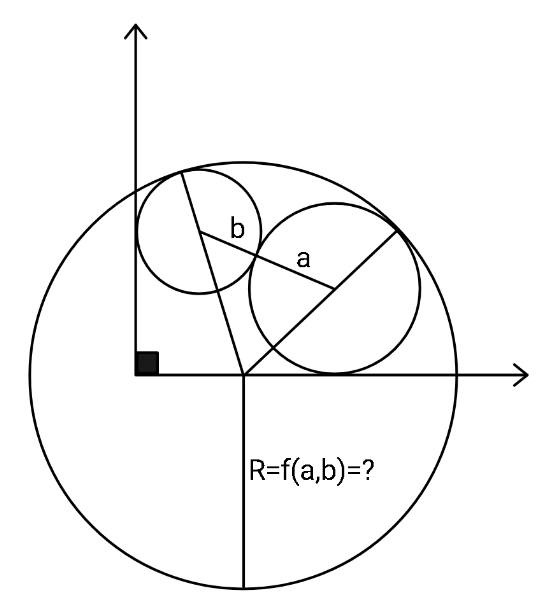
Question Number 158803 by ajfour last updated on 09/Nov/21
Commented by ajfour last updated on 09/Nov/21
$$\:\:\:\:\:\:\:\:\:\:\:\:{Q}.\mathrm{158749}\:\:{again} \\ $$
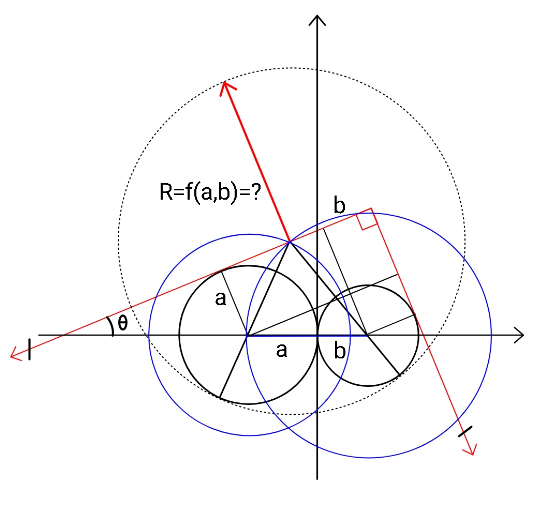
Answered by ajfour last updated on 09/Nov/21
Commented by ajfour last updated on 09/Nov/21
![Let (a/(sin θ))=p condider T(−h,k) on it. (k/(p+a−h))=tan θ=m (a−h)^2 +(p+a−h)^2 m^2 =(r−a)^2 (b+h)^2 +(p+a−h)^2 m^2 =(r−b)^2 subtracting (a−b−2h)(a+b) =(2r−a−b)(b−a) 2r=a+b+(((a+b)/(a−b))){2h−(a−b)} ((d(2r))/dh)=2(((a+b)/(a−b))) [constant>0] but limits of h is difficult to guess. ......](https://www.tinkutara.com/question/Q158820.png)
$${Let}\:\:\frac{{a}}{\mathrm{sin}\:\theta}={p} \\ $$$${condider}\:{T}\left(−{h},{k}\right)\:{on}\:{it}. \\ $$$$\frac{{k}}{{p}+{a}−{h}}=\mathrm{tan}\:\theta={m} \\ $$$$\left({a}−{h}\right)^{\mathrm{2}} +\left({p}+{a}−{h}\right)^{\mathrm{2}} {m}^{\mathrm{2}} =\left({r}−{a}\right)^{\mathrm{2}} \\ $$$$\left({b}+{h}\right)^{\mathrm{2}} +\left({p}+{a}−{h}\right)^{\mathrm{2}} {m}^{\mathrm{2}} =\left({r}−{b}\right)^{\mathrm{2}} \\ $$$${subtracting} \\ $$$$\left({a}−{b}−\mathrm{2}{h}\right)\left({a}+{b}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{2}{r}−{a}−{b}\right)\left({b}−{a}\right) \\ $$$$\mathrm{2}{r}={a}+{b}+\left(\frac{{a}+{b}}{{a}−{b}}\right)\left\{\mathrm{2}{h}−\left({a}−{b}\right)\right\} \\ $$$$\frac{{d}\left(\mathrm{2}{r}\right)}{{dh}}=\mathrm{2}\left(\frac{{a}+{b}}{{a}−{b}}\right)\:\:\:\left[{constant}>\mathrm{0}\right] \\ $$$${but}\:{limits}\:{of}\:\boldsymbol{{h}}\:{is}\:{difficult}\:{to} \\ $$$${guess}. \\ $$$$…… \\ $$
