Question Number 163263 by Ar Brandon last updated on 05/Jan/22
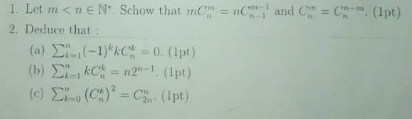
Answered by qaz last updated on 05/Jan/22
^n Σ_(k=0) ^n ((n),(k) )z^k =[z^n ](1+z)^(2n) = (((2n)),(( n)) )_(By Egyolychev′s method)](https://www.tinkutara.com/question/Q163274.png)
$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{k}} \mathrm{k}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}=\frac{\partial}{\partial\mathrm{x}}\mid_{\mathrm{x}=\mathrm{1}} \left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}\left(−\mathrm{x}\right)^{\mathrm{k}} −\mathrm{1}\right)=\frac{\partial}{\partial\mathrm{x}}\mid_{\mathrm{x}=\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}} =−\mathrm{n}\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \mid_{\mathrm{x}=\mathrm{1}} =\mathrm{0} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{k}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}=\frac{\partial}{\partial\mathrm{x}}\mid_{\mathrm{x}=\mathrm{1}} \left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}\mathrm{x}^{\mathrm{k}} −\mathrm{1}\right)=\frac{\partial}{\partial\mathrm{x}}\mid_{\mathrm{x}=\mathrm{1}} \left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} =\mathrm{n}\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \mid_{\mathrm{x}=\mathrm{1}} =\mathrm{n2}^{\mathrm{n}−\mathrm{1}} \\ $$$$\underset{\mathrm{By}\:\mathrm{Egyolychev}'\mathrm{s}\:\mathrm{method}} {\underbrace{\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}^{\mathrm{2}} =\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}\begin{pmatrix}{\:\:\:\mathrm{n}}\\{\mathrm{n}−\mathrm{k}}\end{pmatrix}=\left[\mathrm{z}^{\mathrm{n}} \right]\left(\mathrm{1}+\mathrm{z}\right)^{\mathrm{n}} \underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\begin{pmatrix}{\mathrm{n}}\\{\mathrm{k}}\end{pmatrix}\mathrm{z}^{\mathrm{k}} =\left[\mathrm{z}^{\mathrm{n}} \right]\left(\mathrm{1}+\mathrm{z}\right)^{\mathrm{2n}} =\begin{pmatrix}{\mathrm{2n}}\\{\:\mathrm{n}}\end{pmatrix}}} \\ $$
Commented by Ar Brandon last updated on 06/Jan/22
thanks
