Question Number 16364 by Tinkutara last updated on 21/Jun/17
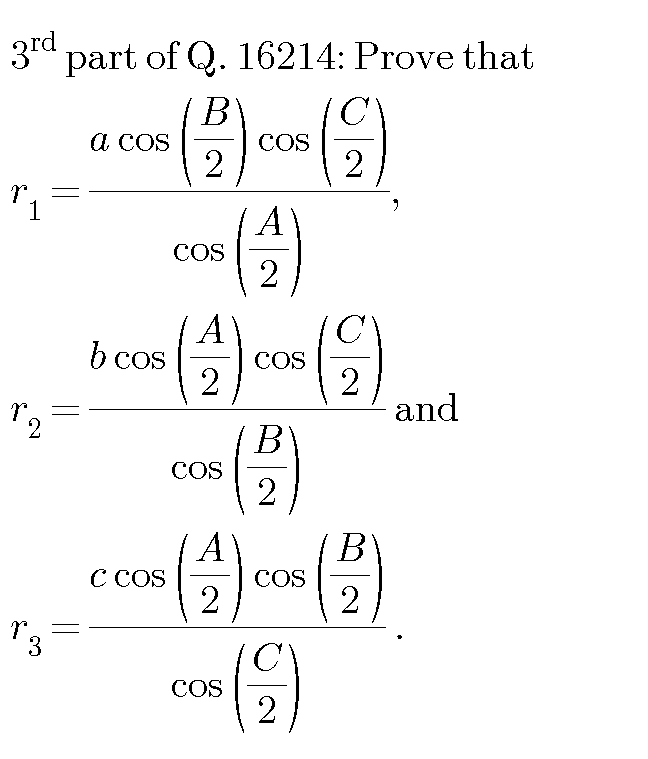
Answered by ajfour last updated on 21/Jun/17
Commented by ajfour last updated on 21/Jun/17
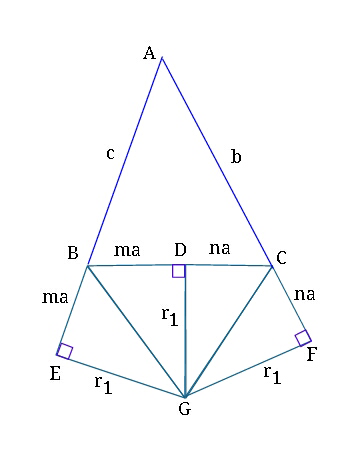
![In △BCG , applying the sine rule : first the angles, ∠CBG=(π/2)−(B/2) , ∠BGC=(B/2)+(C/2) ∠CGD = C/2 ⇒CG= (r_1 /(cos (C/2))) ((CG)/(sin ∠CBG)) = ((BC)/(sin ∠BGC)) (([r_1 /cos (C/2)])/(sin (π/2−B/2))) =(a/(sin (B/2+C/2))) (r_1 /(cos (B/2)cos (C/2))) = (a/(sin ((π/2)−(A/2)))) ⇒ r_1 = ((acos (B/2)cos (C/2))/(cos (A/2))) . similarly for r_2 , and r_3 .](https://www.tinkutara.com/question/Q16375.png)
$${In}\:\bigtriangleup{BCG}\:,\:{applying}\:{the}\:{sine}\:{rule}\:: \\ $$$${first}\:{the}\:{angles}, \\ $$$$\:\angle{CBG}=\frac{\pi}{\mathrm{2}}−\frac{{B}}{\mathrm{2}}\:,\:\angle{BGC}=\frac{{B}}{\mathrm{2}}+\frac{{C}}{\mathrm{2}} \\ $$$$\angle{CGD}\:=\:{C}/\mathrm{2}\:\:\Rightarrow{CG}=\:\frac{{r}_{\mathrm{1}} }{\mathrm{cos}\:\left({C}/\mathrm{2}\right)} \\ $$$$\:\frac{{CG}}{\mathrm{sin}\:\angle{CBG}}\:=\:\frac{{BC}}{\mathrm{sin}\:\angle{BGC}} \\ $$$$\:\frac{\left[{r}_{\mathrm{1}} /\mathrm{cos}\:\left({C}/\mathrm{2}\right)\right]}{\mathrm{sin}\:\left(\pi/\mathrm{2}−{B}/\mathrm{2}\right)}\:=\frac{{a}}{\mathrm{sin}\:\left({B}/\mathrm{2}+{C}/\mathrm{2}\right)} \\ $$$$\:\frac{{r}_{\mathrm{1}} }{\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}}}\:=\:\frac{{a}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\frac{{A}}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\:\:{r}_{\mathrm{1}} \:=\:\frac{{a}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}}}{\mathrm{cos}\:\frac{{A}}{\mathrm{2}}}\:\:. \\ $$$$\:{similarly}\:{for}\:{r}_{\mathrm{2}} ,\:{and}\:{r}_{\mathrm{3}} \:. \\ $$
Commented by Tinkutara last updated on 21/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
