Question Number 165795 by mnjuly1970 last updated on 08/Feb/22
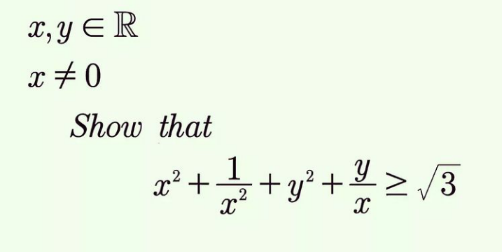
Answered by ArielVyny last updated on 08/Feb/22
![soit f(x,y)=x^2 +(1/x^2 )+y^2 +(y/x) montrons que f(x,y)≥(√3) x≠0 -fixons x∈R on a f_x (y)=x^2 +(1/x^2 )+y^2 +y(1/x) f_x (y)=(y+(1/(2x)))^2 −(1/(4x^2 ))+x^2 +(1/x^2 ) =(y+(1/(2x)))^2 +(3/(4x^2 ))+x^2 α=(1/(2x))→x=(1/(2α)) f_x (y)=(y+α)^2 +3α^2 +(1/(4α^2 )) posons α^2 ∈[0;1] on a 3α^2 +(1/(4α^2 ))≥(√3) de meme pour α^2 ∈]1;+∞[ 3α^2 +(1/(4α^2 ))≥(√3) de plus cbaque terme de f_x (y) est positif donc f_x (y)≥(√3) -fixons y f_y (x)=x^2 +(1/x^2 )+(y/x)+y^2 (x≠0) f_y (x)=(x−(1/x))^2 +y^2 +2+(y/x) =(x−(1/x))^2 +(y+(1/(2x)))^2 −(1/(2x^2 ))+2 par raisonnement analogue on trouve l′inegalite NB on pourra etudier q(x)=−(1/(2x^2 ))+2−(√3) extraire l′inerval ou q(x) est negatif et montrerque si l′on ajoute (x−(1/x))^2 +(y+(1/(2x)))^2 f_y (x)≥(√3)](https://www.tinkutara.com/question/Q165810.png)
$${soit}\:{f}\left({x},{y}\right)={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{y}^{\mathrm{2}} +\frac{{y}}{{x}} \\ $$$${montrons}\:{que}\:{f}\left({x},{y}\right)\geqslant\sqrt{\mathrm{3}}\:\:{x}\neq\mathrm{0} \\ $$$$-{fixons}\:{x}\in\mathbb{R}\:{on}\:{a}\:{f}_{{x}} \left({y}\right)={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{y}^{\mathrm{2}} +{y}\frac{\mathrm{1}}{{x}} \\ $$$${f}_{{x}} \left({y}\right)=\left({y}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }+{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left({y}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} }+{x}^{\mathrm{2}} \\ $$$$\alpha=\frac{\mathrm{1}}{\mathrm{2}{x}}\rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}\alpha} \\ $$$${f}_{{x}} \left({y}\right)=\left({y}+\alpha\right)^{\mathrm{2}} +\mathrm{3}\alpha^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} } \\ $$$${posons}\:\alpha^{\mathrm{2}} \in\left[\mathrm{0};\mathrm{1}\right]\:\:{on}\:{a}\:\mathrm{3}\alpha^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} }\geqslant\sqrt{\mathrm{3}} \\ $$$$\left.{de}\:{meme}\:{pour}\:\alpha^{\mathrm{2}} \in\right]\mathrm{1};+\infty\left[\:\mathrm{3}\alpha^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}\alpha^{\mathrm{2}} }\geqslant\sqrt{\mathrm{3}}\right. \\ $$$${de}\:{plus}\:{cbaque}\:{terme}\:{de}\:{f}_{{x}} \left({y}\right)\:{est}\:{positif}\:{donc} \\ $$$${f}_{{x}} \left({y}\right)\geqslant\sqrt{\mathrm{3}} \\ $$$$-{fixons}\:{y}\:\:{f}_{{y}} \left({x}\right)={x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{{y}}{{x}}+{y}^{\mathrm{2}} \:\:\:\left({x}\neq\mathrm{0}\right) \\ $$$${f}_{{y}} \left({x}\right)=\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}+\frac{{y}}{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{2} \\ $$$${par}\:{raisonnement}\:{analogue}\:{on}\:{trouve}\:{l}'{inegalite} \\ $$$${NB}\:{on}\:{pourra}\:{etudier}\:{q}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }+\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${extraire}\:{l}'{inerval}\:{ou}\:{q}\left({x}\right)\:{est}\:{negatif} \\ $$$${et}\:{montrerque}\:{si}\:{l}'{on}\:{ajoute}\:\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{1}}{\mathrm{2}{x}}\right)^{\mathrm{2}} \\ $$$${f}_{{y}} \left({x}\right)\geqslant\sqrt{\mathrm{3}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 09/Feb/22
$${very}\:{nice}\:{thank}\:{you}\:{sir} \\ $$
Answered by mr W last updated on 08/Feb/22
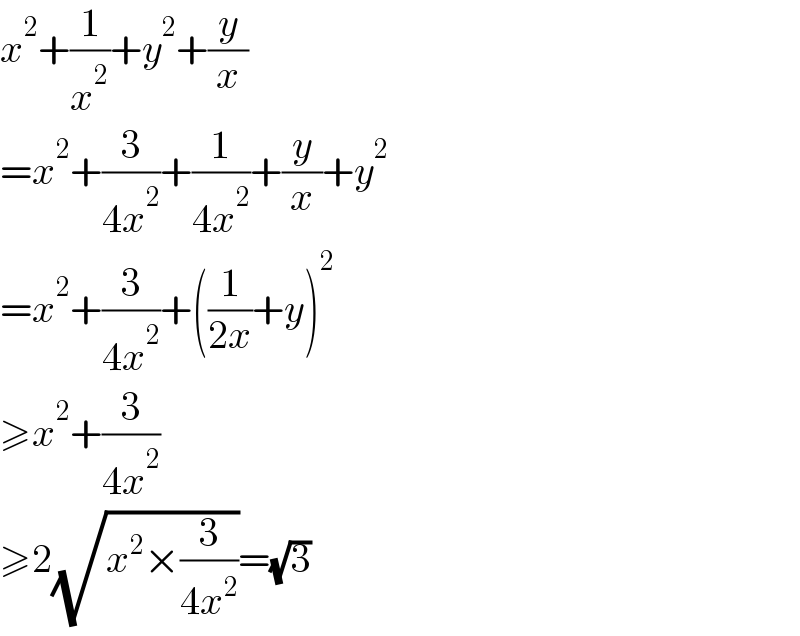
$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{y}^{\mathrm{2}} +\frac{{y}}{{x}} \\ $$$$={x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}{x}^{\mathrm{2}} }+\frac{{y}}{{x}}+{y}^{\mathrm{2}} \\ $$$$={x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} }+\left(\frac{\mathrm{1}}{\mathrm{2}{x}}+{y}\right)^{\mathrm{2}} \\ $$$$\geqslant{x}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} } \\ $$$$\geqslant\mathrm{2}\sqrt{{x}^{\mathrm{2}} ×\frac{\mathrm{3}}{\mathrm{4}{x}^{\mathrm{2}} }}=\sqrt{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 09/Feb/22
$$\:\:\:\:{thanks}\:{alot}\:{sir}\:\mathrm{W} \\ $$
