Question Number 168338 by infinityaction last updated on 08/Apr/22
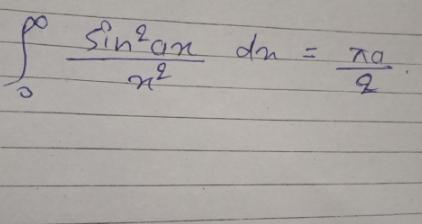
Answered by Mathspace last updated on 08/Apr/22
![∫_0 ^∞ ((sin^2 (ax))/x^2 )dx a>0 =_(ax=t) ∫_0 ^∞ ((sin^2 (t))/(((t/a))^2 ))(dt/a) =a∫_0 ^∞ ((sin^2 t)/t^2 )dt by parts ∫_0 ^∞ ((sin^2 t)/t^2 )dt=[−(1/t)sin^2 t]_0 ^(→∞) +∫_0 ^∞ (1/t)(2sint.cost)dt =0+∫_0 ^∞ ((sin(2t))/t)dt (2t=z) =2∫_0 ^∞ ((sinz)/z)(dz/2)=∫_0 ^∞ ((sinz)/z)dz=(π/2) ⇒ ∫_0 ^∞ ((sin^2 (ax))/x^2 )dx=((πa)/2) if a<0 we get the same result due?to x→((sin^2 (ax))/x^2 ) is even](https://www.tinkutara.com/question/Q168351.png)
$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}^{\mathrm{2}} \left({ax}\right)}{{x}^{\mathrm{2}} }{dx}\:\:\:\:{a}>\mathrm{0} \\ $$$$=_{{ax}={t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}^{\mathrm{2}} \left({t}\right)}{\left(\frac{{t}}{{a}}\right)^{\mathrm{2}} }\frac{{dt}}{{a}} \\ $$$$={a}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} }{dt}\:\:{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} }{dt}=\left[−\frac{\mathrm{1}}{{t}}{sin}^{\mathrm{2}} {t}\right]_{\mathrm{0}} ^{\rightarrow\infty} \\ $$$$+\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{t}}\left(\mathrm{2}{sint}.{cost}\right){dt} \\ $$$$=\mathrm{0}+\int_{\mathrm{0}} ^{\infty} \:\:\frac{{sin}\left(\mathrm{2}{t}\right)}{{t}}{dt}\:\:\left(\mathrm{2}{t}={z}\right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{{sinz}}{{z}}\frac{{dz}}{\mathrm{2}}=\int_{\mathrm{0}} ^{\infty} \:\frac{{sinz}}{{z}}{dz}=\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}^{\mathrm{2}} \left({ax}\right)}{{x}^{\mathrm{2}} }{dx}=\frac{\pi{a}}{\mathrm{2}} \\ $$$${if}\:{a}<\mathrm{0}\:{we}\:{get}\:{the}\:{same}\:{result}\: \\ $$$${due}?{to}\:\:{x}\rightarrow\frac{{sin}^{\mathrm{2}} \left({ax}\right)}{{x}^{\mathrm{2}} }\:{is}\:{even} \\ $$$$ \\ $$$$ \\ $$
Commented by infinityaction last updated on 08/Apr/22

$${thank}\:{you}\:{sir} \\ $$
