Question Number 172443 by SANOGO last updated on 27/Jun/22

Answered by Mathspace last updated on 27/Jun/22
![2) la fonctionx→ Υ(x,t) est derivable surR et (∂/∂x)Ψ(x,t)=(e^(−at) −e^(−bt) )cos(xt) t→(((e^(−at) −e^(−bt) )cos(xt))/t) est integrable sur ]o,+∞[ ∣(∂Ψ/∂x)∣=∣e^(−at) −e^(−bt) )cos(xt)∣ ≤∣e^(−at) −e^(−bt) ∣≤e^(−at) +e^(−bt) et ∫_0 ^∞ (e^(−at) +e^(−bt) )dt<∞ ⇒ f est derivable et 23et4)(∂f/∂x)=∫_0 ^∞ (e^(−at) −e^(−bt) )cos(xt)dt =Re(∫_0 ^∞ (e^(−at) −e^(−bt) )e^(ixt) dt) =Re(∫_0 ^∞ (e^((−a+ix)t) −e^((−b+ix)t) )dt) on a ∫_0 ^∞ (....)dt =[(1/(−a+ix))e^((−a+ix)t) −(1/(−b+ix))e^((−b+ix)t) ]_0 ^(+∞) =−(1/(−a+ix))+(1/(−b+ix)) =(1/(a−ix))−(1/(b−ix)) =((a+ix)/(a^2 +x^2 ))−((b+ix)/(b^2 +x^2 )) =(a/(x^2 +a^2 ))−(b/(x^2 +b^2 )) +i(....) ⇒ Re(∫ ....)=(a/(x^2 +a^2 ))−(b/(x^2 +b^2 )) =f^′ (x)⇒f(x)=∫ ((adx)/(x^2 +a^2 ))(→x=ay) −∫ ((bdx)/(x^2 +b^2 ))(→x=bz) =∫ (dy/(1+y^2 ))−∫ (dz/(1+z^2 )) =arctan(y)−arctan(z) +C =(arctan((x/a)))−arctan((x/b)) +C C=lim_(x→+∞) f(x) changdment xt=z donne ∫_0 ^∞ (((e^(−at) −e^(−bt) )cos(xt))/t)dt =∫_0 ^∞ (((e^(−a(z/x)) −e^(−b(z/x)) )cosz)/(z/x))(dz/x) =∫_0 ^∞ ((cosz)/z)(e^(−a(z/x)) −e^(−b(z/x)) )dz ∃m>0 /∣f(x)∣<(m/x)→0 (x→+∞) ⇒ C=0 ⇒f(x)=arctan((x/a))−arctan((x/b)) on tan(....)=(((x/a)−(x/b))/(1+(x/a).(x/b))) =((((b−a)/(ab))x)/(1+(x^2 /(ab))))=(((b−a)x)/(x^2 +ab)) ⇒ f(x)=arctan((((b−a)x)/(x^2 +ab)))](https://www.tinkutara.com/question/Q172479.png)
$$\left.\mathrm{2}\right)\:{la}\:{fonctionx}\rightarrow\:\Upsilon\left({x},{t}\right)\:{est}\:{derivable}\:{surR} \\ $$$${et}\:\frac{\partial}{\partial{x}}\Psi\left({x},{t}\right)=\left({e}^{−{at}} −{e}^{−{bt}} \right){cos}\left({xt}\right) \\ $$$${t}\rightarrow\frac{\left({e}^{−{at}} −{e}^{−{bt}} \right){cos}\left({xt}\right)}{{t}}\:{est}\:{integrable} \\ $$$$\left.{sur}\:\:\right]{o},+\infty\left[\right. \\ $$$$\left.\mid\frac{\partial\Psi}{\partial{x}}\mid=\mid{e}^{−{at}} −{e}^{−{bt}} \right){cos}\left({xt}\right)\mid \\ $$$$\leqslant\mid{e}^{−{at}} −{e}^{−{bt}} \mid\leqslant{e}^{−{at}} +{e}^{−{bt}} \:{et} \\ $$$$\int_{\mathrm{0}} ^{\infty} \left({e}^{−{at}} +{e}^{−{bt}} \right){dt}<\infty\:\Rightarrow \\ $$$${f}\:{est}\:{derivable}\:{et} \\ $$$$\left.\mathrm{23}{et}\mathrm{4}\right)\frac{\partial{f}}{\partial{x}}=\int_{\mathrm{0}} ^{\infty} \left({e}^{−{at}} −{e}^{−{bt}} \right){cos}\left({xt}\right){dt} \\ $$$$={Re}\left(\int_{\mathrm{0}} ^{\infty} \left({e}^{−{at}} −{e}^{−{bt}} \right){e}^{{ixt}} {dt}\right) \\ $$$$={Re}\left(\int_{\mathrm{0}} ^{\infty} \left({e}^{\left(−{a}+{ix}\right){t}} −{e}^{\left(−{b}+{ix}\right){t}} \right){dt}\right) \\ $$$${on}\:{a}\:\int_{\mathrm{0}} ^{\infty} \left(….\right){dt} \\ $$$$=\left[\frac{\mathrm{1}}{−{a}+{ix}}{e}^{\left(−{a}+{ix}\right){t}} −\frac{\mathrm{1}}{−{b}+{ix}}{e}^{\left(−{b}+{ix}\right){t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=−\frac{\mathrm{1}}{−{a}+{ix}}+\frac{\mathrm{1}}{−{b}+{ix}} \\ $$$$=\frac{\mathrm{1}}{{a}−{ix}}−\frac{\mathrm{1}}{{b}−{ix}} \\ $$$$=\frac{{a}+{ix}}{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} }−\frac{{b}+{ix}}{{b}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$=\frac{{a}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }−\frac{{b}}{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:+{i}\left(….\right)\:\Rightarrow \\ $$$${Re}\left(\int\:\:….\right)=\frac{{a}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }−\frac{{b}}{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }\: \\ $$$$={f}^{'} \left({x}\right)\Rightarrow{f}\left({x}\right)=\int\:\:\frac{{adx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }\left(\rightarrow{x}={ay}\right) \\ $$$$−\int\:\frac{{bdx}}{{x}^{\mathrm{2}} +{b}^{\mathrm{2}} }\left(\rightarrow{x}={bz}\right) \\ $$$$=\int\:\:\frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} }−\int\:\frac{{dz}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$$={arctan}\left({y}\right)−{arctan}\left({z}\right)\:+{C} \\ $$$$=\left({arctan}\left(\frac{{x}}{{a}}\right)\right)−{arctan}\left(\frac{{x}}{{b}}\right)\:+{C} \\ $$$${C}={lim}_{{x}\rightarrow+\infty} {f}\left({x}\right) \\ $$$${changdment}\:{xt}={z}\:{donne} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left({e}^{−{at}} −{e}^{−{bt}} \right){cos}\left({xt}\right)}{{t}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left({e}^{−{a}\frac{{z}}{{x}}} −{e}^{−{b}\frac{{z}}{{x}}} \right){cosz}}{\frac{{z}}{{x}}}\frac{{dz}}{{x}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cosz}}{{z}}\left({e}^{−{a}\frac{{z}}{{x}}} −{e}^{−{b}\frac{{z}}{{x}}} \right){dz} \\ $$$$\exists{m}>\mathrm{0}\:/\mid{f}\left({x}\right)\mid<\frac{{m}}{{x}}\rightarrow\mathrm{0}\:\left({x}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${C}=\mathrm{0}\:\Rightarrow{f}\left({x}\right)={arctan}\left(\frac{{x}}{{a}}\right)−{arctan}\left(\frac{{x}}{{b}}\right) \\ $$$${on}\:{tan}\left(….\right)=\frac{\frac{{x}}{{a}}−\frac{{x}}{{b}}}{\mathrm{1}+\frac{{x}}{{a}}.\frac{{x}}{{b}}} \\ $$$$=\frac{\frac{{b}−{a}}{{ab}}{x}}{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{{ab}}}=\frac{\left({b}−{a}\right){x}}{{x}^{\mathrm{2}} +{ab}}\:\Rightarrow \\ $$$${f}\left({x}\right)={arctan}\left(\frac{\left({b}−{a}\right){x}}{{x}^{\mathrm{2}} +{ab}}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by Mathspace last updated on 27/Jun/22
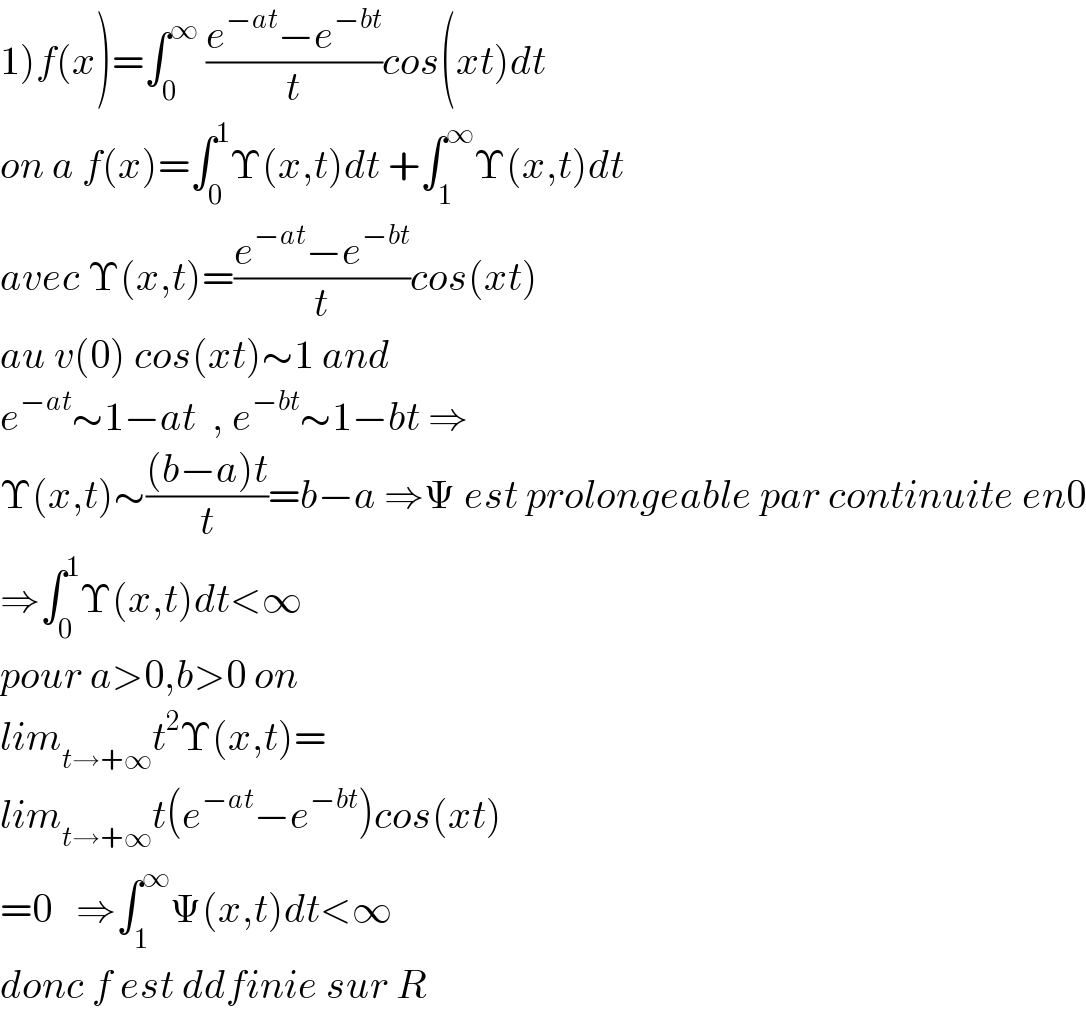
$$\left.\mathrm{1}\right){f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{at}} −{e}^{−{bt}} }{{t}}{cos}\left({xt}\right){dt} \\ $$$${on}\:{a}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \Upsilon\left({x},{t}\right){dt}\:+\int_{\mathrm{1}} ^{\infty} \Upsilon\left({x},{t}\right){dt} \\ $$$${avec}\:\Upsilon\left({x},{t}\right)=\frac{{e}^{−{at}} −{e}^{−{bt}} }{{t}}{cos}\left({xt}\right) \\ $$$${au}\:{v}\left(\mathrm{0}\right)\:{cos}\left({xt}\right)\sim\mathrm{1}\:{and} \\ $$$${e}^{−{at}} \sim\mathrm{1}−{at}\:\:,\:{e}^{−{bt}} \sim\mathrm{1}−{bt}\:\Rightarrow \\ $$$$\Upsilon\left({x},{t}\right)\sim\frac{\left({b}−{a}\right){t}}{{t}}={b}−{a}\:\Rightarrow\Psi\:{est}\:{prolongeable}\:{par}\:{continuite}\:{en}\mathrm{0} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \Upsilon\left({x},{t}\right){dt}<\infty \\ $$$${pour}\:{a}>\mathrm{0},{b}>\mathrm{0}\:{on}\: \\ $$$${lim}_{{t}\rightarrow+\infty} {t}^{\mathrm{2}} \Upsilon\left({x},{t}\right)= \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\left({e}^{−{at}} −{e}^{−{bt}} \right){cos}\left({xt}\right) \\ $$$$=\mathrm{0}\:\:\:\Rightarrow\int_{\mathrm{1}} ^{\infty} \Psi\left({x},{t}\right){dt}<\infty \\ $$$${donc}\:{f}\:{est}\:{ddfinie}\:{sur}\:{R} \\ $$
