Question Number 173807 by mokys last updated on 18/Jul/22
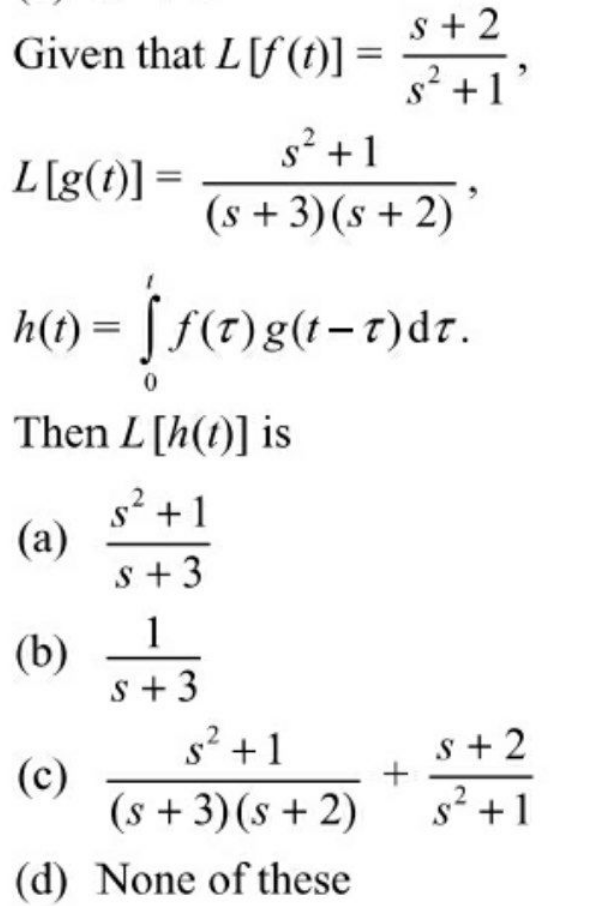
Answered by aleks041103 last updated on 18/Jul/22
![h(t)=∫_0 ^( t) f(x)g(t−x)dx h is the convolution of f and g. for convolution and the laplace transform it′s true that: L[h]=L[f]L[g] ⇒L[h]=((s+2)/(s^2 +1)) ((s^2 +1)/((s+3)(s+2))) ⇒L[h](s)=(1/(s+3))](https://www.tinkutara.com/question/Q173808.png)
$${h}\left({t}\right)=\underset{\mathrm{0}} {\overset{\:{t}} {\int}}{f}\left({x}\right){g}\left({t}−{x}\right){dx} \\ $$$${h}\:{is}\:{the}\:{convolution}\:{of}\:{f}\:{and}\:{g}. \\ $$$${for}\:{convolution}\:{and}\:{the}\:{laplace}\:{transform} \\ $$$${it}'{s}\:{true}\:{that}: \\ $$$${L}\left[{h}\right]={L}\left[{f}\right]{L}\left[{g}\right] \\ $$$$\Rightarrow{L}\left[{h}\right]=\frac{{s}+\mathrm{2}}{{s}^{\mathrm{2}} +\mathrm{1}}\:\frac{{s}^{\mathrm{2}} +\mathrm{1}}{\left({s}+\mathrm{3}\right)\left({s}+\mathrm{2}\right)} \\ $$$$\Rightarrow{L}\left[{h}\right]\left({s}\right)=\frac{\mathrm{1}}{{s}+\mathrm{3}} \\ $$
