Menu Close

Question-174728

Tinku Tara 0 Comments
Pin




Question Number 174728 by ajfour last updated on 09/Aug/22
Commented by ajfour last updated on 09/Aug/22
If rod is released as shown and rod rolls over the fixed semi- cylinder how long does it take for end B to strike the ground, the other side?
$${If}\:{rod}\:{is}\:{released}\:{as}\:{shown}\:{and} \\ $$$${rod}\:{rolls}\:{over}\:{the}\:{fixed}\:{semi}- \\ $$$${cylinder}\:{how}\:{long}\:{does}\:{it}\:{take}\:{for} \\ $$$$\:{end}\:{B}\:{to}\:{strike}\:{the}\:{ground},\:{the}\: \\ $$$${other}\:{side}? \\ $$
Commented by mr W last updated on 14/Aug/22
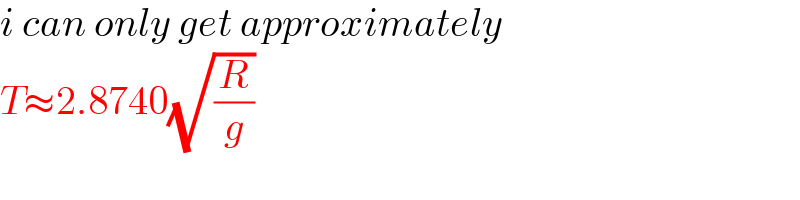
i can only get approximately T≈2.8740(√(R/g))
$${i}\:{can}\:{only}\:{get}\:{approximately} \\ $$$${T}\approx\mathrm{2}.\mathrm{8740}\sqrt{\frac{{R}}{{g}}} \\ $$
Commented by ajfour last updated on 14/Aug/22
Immense work and guidance, sir, i shall check carefully.
$${Immense}\:{work}\:{and}\:{guidance}, \\ $$$${sir},\:{i}\:{shall}\:{check}\:{carefully}. \\ $$
Answered by mr W last updated on 13/Aug/22
Commented by mr W last updated on 15/Aug/22
AB=L=4R AC=a−Rθ I_C =((L^2 m)/(12))+((L/2)−a+Rθ)^2 m let b=(L/2)−a I_C =((L^2 m)/(12))+(b+Rθ)^2 m y_M =R sin θ−(b+Rθ)cos θ ((I_C ω^2 )/2)=mg(((4R)/3)−R sin θ+(b+Rθ)cos θ) (ω^2 /2)[((L^2 m)/(12))+(b+Rθ)^2 m]=mg(((4R)/3)−R sin θ+(b+Rθ)cos θ) ω^2 [(4/3)+((b/R)+θ)^2 ]=((2g)/R)[(4/3)−sin θ+((b/R)+θ)cos θ] ω=−(dθ/dt)=(√((2g)/R))(√(((4/3)−sin θ+((b/R)+θ)cos θ)/((4/3)+((b/R)+θ)^2 ))) ∫_0 ^T dt=(√(R/(2g)))∫_θ_1 ^θ_0 (√(((4/3)+((b/R)+θ)^2 )/((4/3)−sin θ+((b/R)+θ)cos θ))) dθ T=(√(R/(2g)))∫_θ_1 ^θ_0 (√(((4/3)+((b/R)+θ)^2 )/((4/3)−sin θ+((b/R)+θ)cos θ))) dθ T=(√(R/(2g)))∫_θ_1 ^θ_0 (√(((4/3)+[θ−(((π+(√5))/2)+sin^(−1) (2/3)−2)]^2 )/((4/3)−sin θ+[θ−(((π+(√5))/2)+sin^(−1) (2/3)−2)]cos θ))) dθ T=(√(R/(2g)))∫_(1.0097) ^(2.3005) (√(((4/3)+(θ−1.418558)^2 )/((4/3)−sin θ+(θ−1.418558)cos θ))) dθ T≈2.8740(√(R/g))
$${AB}={L}=\mathrm{4}{R} \\ $$$${AC}={a}−{R}\theta \\ $$$${I}_{{C}} =\frac{{L}^{\mathrm{2}} {m}}{\mathrm{12}}+\left(\frac{{L}}{\mathrm{2}}−{a}+{R}\theta\right)^{\mathrm{2}} {m} \\ $$$${let}\:{b}=\frac{{L}}{\mathrm{2}}−{a} \\ $$$${I}_{{C}} =\frac{{L}^{\mathrm{2}} {m}}{\mathrm{12}}+\left({b}+{R}\theta\right)^{\mathrm{2}} {m} \\ $$$${y}_{{M}} ={R}\:\mathrm{sin}\:\theta−\left({b}+{R}\theta\right)\mathrm{cos}\:\theta \\ $$$$\frac{{I}_{{C}} \omega^{\mathrm{2}} }{\mathrm{2}}={mg}\left(\frac{\mathrm{4}{R}}{\mathrm{3}}−{R}\:\mathrm{sin}\:\theta+\left({b}+{R}\theta\right)\mathrm{cos}\:\theta\right) \\ $$$$\frac{\omega^{\mathrm{2}} }{\mathrm{2}}\left[\frac{{L}^{\mathrm{2}} {m}}{\mathrm{12}}+\left({b}+{R}\theta\right)^{\mathrm{2}} {m}\right]={mg}\left(\frac{\mathrm{4}{R}}{\mathrm{3}}−{R}\:\mathrm{sin}\:\theta+\left({b}+{R}\theta\right)\mathrm{cos}\:\theta\right) \\ $$$$\omega^{\mathrm{2}} \left[\frac{\mathrm{4}}{\mathrm{3}}+\left(\frac{{b}}{{R}}+\theta\right)^{\mathrm{2}} \right]=\frac{\mathrm{2}{g}}{{R}}\left[\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{sin}\:\theta+\left(\frac{{b}}{{R}}+\theta\right)\mathrm{cos}\:\theta\right] \\ $$$$\omega=−\frac{{d}\theta}{{dt}}=\sqrt{\frac{\mathrm{2}{g}}{{R}}}\sqrt{\frac{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{sin}\:\theta+\left(\frac{{b}}{{R}}+\theta\right)\mathrm{cos}\:\theta}{\frac{\mathrm{4}}{\mathrm{3}}+\left(\frac{{b}}{{R}}+\theta\right)^{\mathrm{2}} }} \\ $$$$\int_{\mathrm{0}} ^{{T}} {dt}=\sqrt{\frac{{R}}{\mathrm{2}{g}}}\int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{0}} } \sqrt{\frac{\frac{\mathrm{4}}{\mathrm{3}}+\left(\frac{{b}}{{R}}+\theta\right)^{\mathrm{2}} }{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{sin}\:\theta+\left(\frac{{b}}{{R}}+\theta\right)\mathrm{cos}\:\theta}}\:{d}\theta \\ $$$${T}=\sqrt{\frac{{R}}{\mathrm{2}{g}}}\int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{0}} } \sqrt{\frac{\frac{\mathrm{4}}{\mathrm{3}}+\left(\frac{{b}}{{R}}+\theta\right)^{\mathrm{2}} }{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{sin}\:\theta+\left(\frac{{b}}{{R}}+\theta\right)\mathrm{cos}\:\theta}}\:{d}\theta \\ $$$${T}=\sqrt{\frac{{R}}{\mathrm{2}{g}}}\int_{\theta_{\mathrm{1}} } ^{\theta_{\mathrm{0}} } \sqrt{\frac{\frac{\mathrm{4}}{\mathrm{3}}+\left[\theta−\left(\frac{\pi+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}−\mathrm{2}\right)\right]^{\mathrm{2}} }{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{sin}\:\theta+\left[\theta−\left(\frac{\pi+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}−\mathrm{2}\right)\right]\mathrm{cos}\:\theta}}\:{d}\theta \\ $$$${T}=\sqrt{\frac{{R}}{\mathrm{2}{g}}}\int_{\mathrm{1}.\mathrm{0097}} ^{\mathrm{2}.\mathrm{3005}} \sqrt{\frac{\frac{\mathrm{4}}{\mathrm{3}}+\left(\theta−\mathrm{1}.\mathrm{418558}\right)^{\mathrm{2}} }{\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{sin}\:\theta+\left(\theta−\mathrm{1}.\mathrm{418558}\right)\mathrm{cos}\:\theta}}\:{d}\theta \\ $$$${T}\approx\mathrm{2}.\mathrm{8740}\sqrt{\frac{{R}}{{g}}} \\ $$
Commented by ajfour last updated on 14/Aug/22
let centre of semicircle be O. L=2l I_0 =I_m +m{r^2 +(a−rθ)^2 } I_m =((ml^2 )/3) mg{rcos θ+[l−(a−rθ)]sin θ}dt =d{I_0 ((dθ/dt))} g{rcos θ+(l+rθ−a)sin θ}dθ =((dθ/dt))d{[(l^2 /3)+r^2 +(a−rθ)^2 ]((dθ/dt))} here l=2r , a=((√5)/2)r ((g/r)){cos θ+(θ+2−((√5)/2))sin θ}dθ =ωd{[(7/3)+(((√5)/2)−θ)^2 ]ω} MjS sir may let us know with some great calculator θ(t). Given (g/r)=c, boundary value θ=sin^(−1) (2/3) for ω=0.
$${let}\:{centre}\:{of}\:{semicircle}\:{be}\:{O}. \\ $$$${L}=\mathrm{2}{l} \\ $$$${I}_{\mathrm{0}} ={I}_{{m}} +{m}\left\{{r}^{\mathrm{2}} +\left({a}−{r}\theta\right)^{\mathrm{2}} \right\} \\ $$$${I}_{{m}} =\frac{{ml}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${mg}\left\{{r}\mathrm{cos}\:\theta+\left[{l}−\left({a}−{r}\theta\right)\right]\mathrm{sin}\:\theta\right\}{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:={d}\left\{{I}_{\mathrm{0}} \left(\frac{{d}\theta}{{dt}}\right)\right\} \\ $$$${g}\left\{{r}\mathrm{cos}\:\theta+\left({l}+{r}\theta−{a}\right)\mathrm{sin}\:\theta\right\}{d}\theta \\ $$$$\:\:\:\:\:\:\:=\left(\frac{{d}\theta}{{dt}}\right){d}\left\{\left[\frac{{l}^{\mathrm{2}} }{\mathrm{3}}+{r}^{\mathrm{2}} +\left({a}−{r}\theta\right)^{\mathrm{2}} \right]\left(\frac{{d}\theta}{{dt}}\right)\right\} \\ $$$${here}\:\:{l}=\mathrm{2}{r}\:\:,\:{a}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}{r} \\ $$$$\left(\frac{{g}}{{r}}\right)\left\{\mathrm{cos}\:\theta+\left(\theta+\mathrm{2}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\mathrm{sin}\:\theta\right\}{d}\theta \\ $$$$\:\:\:\:\:\:=\omega{d}\left\{\left[\frac{\mathrm{7}}{\mathrm{3}}+\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}−\theta\right)^{\mathrm{2}} \right]\omega\right\} \\ $$$$\:\:{MjS}\:{sir}\:{may}\:{let}\:{us}\:{know} \\ $$$${with}\:{some}\:{great}\:{calculator} \\ $$$$\theta\left({t}\right).\:{Given}\:\frac{{g}}{{r}}={c},\:\:{boundary}\:{value} \\ $$$$\:\:\:\theta=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\:\:{for}\:\:\omega=\mathrm{0}. \\ $$$$ \\ $$
Commented by mr W last updated on 14/Aug/22
Commented by mr W last updated on 14/Aug/22
L=4R θ_0 =(π/2)+sin^(−1) (2/3)≈2.3005 (131.8°) AC=(√((((3R)/2))^2 −R^2 ))=(((√5)R)/2)=a−((π/2)+sin^(−1) (2/3))R (a/R)=((√5)/2)+((π/2)+sin^(−1) (2/3)) b=(L/2)−a (b/R)=−(((π+(√5))/2)+sin^(−1) (2/3)−2) y_M =(R/((3R)/2))×(L/2)=((4R)/3)
$${L}=\mathrm{4}{R} \\ $$$$\theta_{\mathrm{0}} =\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\approx\mathrm{2}.\mathrm{3005}\:\:\left(\mathrm{131}.\mathrm{8}°\right) \\ $$$${AC}=\sqrt{\left(\frac{\mathrm{3}{R}}{\mathrm{2}}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{5}}{R}}{\mathrm{2}}={a}−\left(\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\right){R} \\ $$$$\frac{{a}}{{R}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\left(\frac{\pi}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$${b}=\frac{{L}}{\mathrm{2}}−{a} \\ $$$$\frac{{b}}{{R}}=−\left(\frac{\pi+\sqrt{\mathrm{5}}}{\mathrm{2}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}−\mathrm{2}\right) \\ $$$${y}_{{M}} =\frac{{R}}{\frac{\mathrm{3}{R}}{\mathrm{2}}}×\frac{{L}}{\mathrm{2}}=\frac{\mathrm{4}{R}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 14/Aug/22
Commented by mr W last updated on 14/Aug/22
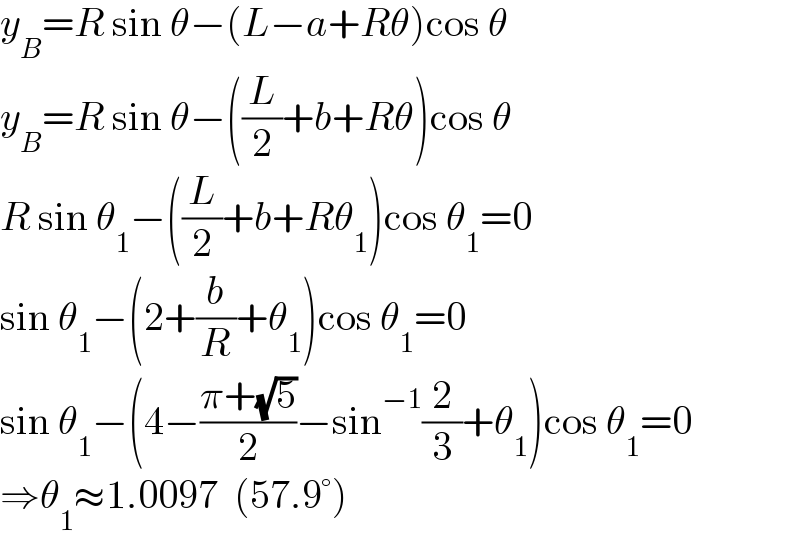
y_B =R sin θ−(L−a+Rθ)cos θ y_B =R sin θ−((L/2)+b+Rθ)cos θ R sin θ_1 −((L/2)+b+Rθ_1 )cos θ_1 =0 sin θ_1 −(2+(b/R)+θ_1 )cos θ_1 =0 sin θ_1 −(4−((π+(√5))/2)−sin^(−1) (2/3)+θ_1 )cos θ_1 =0 ⇒θ_1 ≈1.0097 (57.9°)
$${y}_{{B}} ={R}\:\mathrm{sin}\:\theta−\left({L}−{a}+{R}\theta\right)\mathrm{cos}\:\theta \\ $$$${y}_{{B}} ={R}\:\mathrm{sin}\:\theta−\left(\frac{{L}}{\mathrm{2}}+{b}+{R}\theta\right)\mathrm{cos}\:\theta \\ $$$${R}\:\mathrm{sin}\:\theta_{\mathrm{1}} −\left(\frac{{L}}{\mathrm{2}}+{b}+{R}\theta_{\mathrm{1}} \right)\mathrm{cos}\:\theta_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{sin}\:\theta_{\mathrm{1}} −\left(\mathrm{2}+\frac{{b}}{{R}}+\theta_{\mathrm{1}} \right)\mathrm{cos}\:\theta_{\mathrm{1}} =\mathrm{0} \\ $$$$\mathrm{sin}\:\theta_{\mathrm{1}} −\left(\mathrm{4}−\frac{\pi+\sqrt{\mathrm{5}}}{\mathrm{2}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}}{\mathrm{3}}+\theta_{\mathrm{1}} \right)\mathrm{cos}\:\theta_{\mathrm{1}} =\mathrm{0} \\ $$$$\Rightarrow\theta_{\mathrm{1}} \approx\mathrm{1}.\mathrm{0097}\:\:\left(\mathrm{57}.\mathrm{9}°\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *