Question Number 175860 by Shrinava last updated on 08/Sep/22
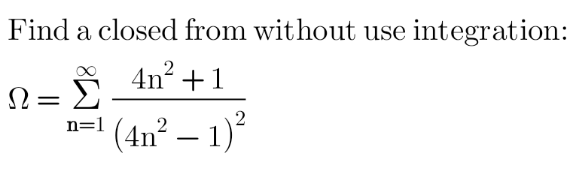
Answered by mr W last updated on 08/Sep/22
![we know: (1/1^2 )+(1/2^2 )+(1/3^2 )+(1/4^2 )+...=(π^2 /6) ((1/1^2 )+(1/3^2 )+(1/5^2 )+...)+((1/2^2 )+(1/4^2 )+(1/6^2 )+...)=(π^2 /6) ((1/1^2 )+(1/3^2 )+(1/5^2 )+...)+(1/4)((1/1^2 )+(1/2^2 )+(1/3^2 )+...)=(π^2 /6) ((1/1^2 )+(1/3^2 )+(1/5^2 )+...)+(1/4)×(π^2 /6)=(π^2 /6) (1/1^2 )+(1/3^2 )+(1/5^2 )+...=(π^2 /8) Σ_(n=1) ^∞ (1/((2n−1)^2 ))=(π^2 /8) Ω=Σ_(n=1) ^∞ ((4n^2 +1)/((4n^2 −1)^2 )) =(1/2)Σ_(n=1) ^∞ [(1/((2n−1)^2 ))+(1/((2n+1)^2 ))] =(1/2)Σ_(n=1) ^∞ [(1/((2n−1)^2 ))+(1/((2n−1)^2 ))]−(1/2) =Σ_(n=1) ^∞ (1/((2n−1)^2 ))−(1/2) =(π^2 /8)−(1/2) ✓](https://www.tinkutara.com/question/Q175869.png)
$${we}\:{know}: \\ $$$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+…=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+…\right)+\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{6}^{\mathrm{2}} }+…\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+…\right)+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+…\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+…\right)+\frac{\mathrm{1}}{\mathrm{4}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{2}} }+…=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$ \\ $$$$\Omega=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}{\left(\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\right]−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}\:\checkmark \\ $$
Commented by Tawa11 last updated on 08/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by mnjuly1970 last updated on 08/Sep/22
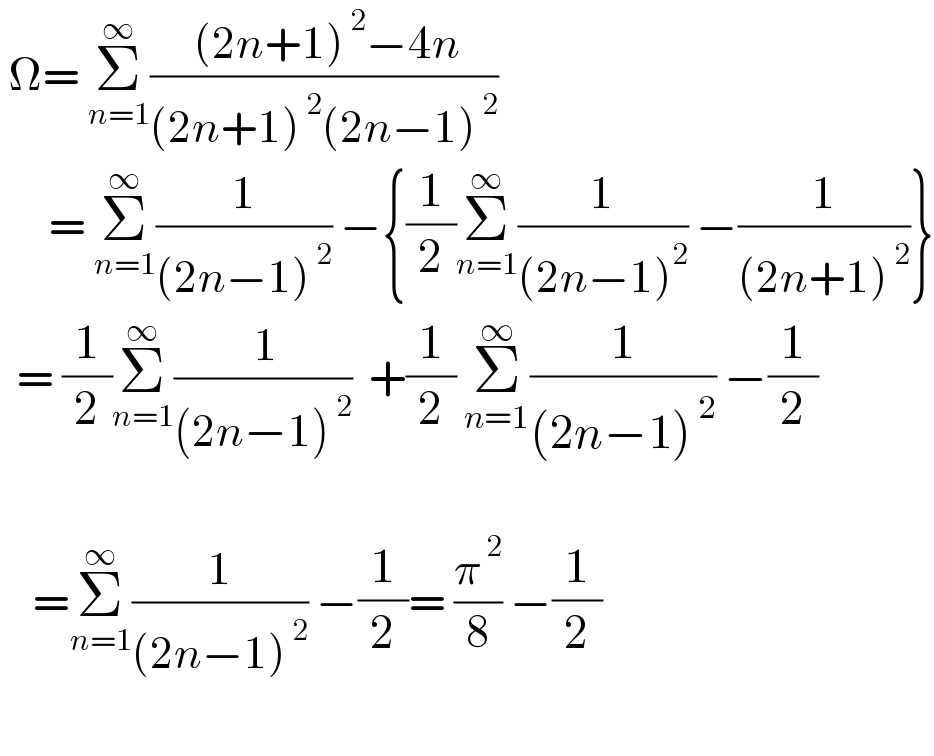
$$\:\Omega=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\left(\mathrm{2}{n}+\mathrm{1}\right)^{\:\mathrm{2}} −\mathrm{4}{n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\:\mathrm{2}} \left(\mathrm{2}{n}−\mathrm{1}\right)^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\:\mathrm{2}} }\:−\left\{\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\:\mathrm{2}} }\right\} \\ $$$$\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\:\mathrm{2}} }\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\:\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\:\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\:\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}=\:\frac{\pi^{\:\mathrm{2}} }{\mathrm{8}}\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 15/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
