Question Number 178037 by mr W last updated on 12/Oct/22
Commented by mr W last updated on 12/Oct/22
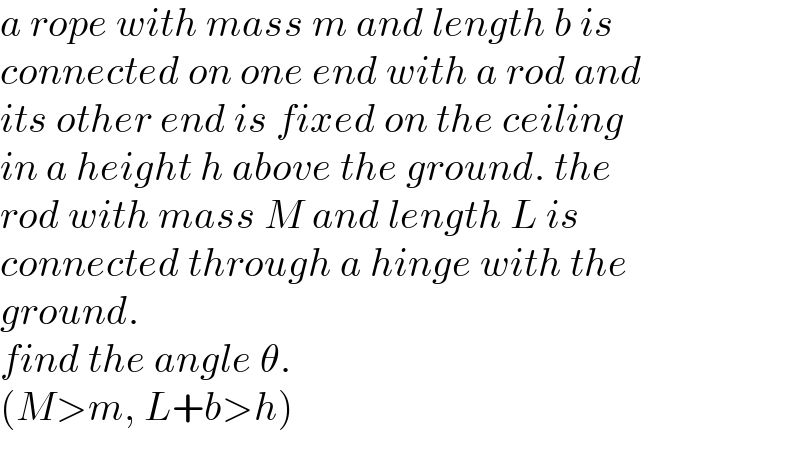
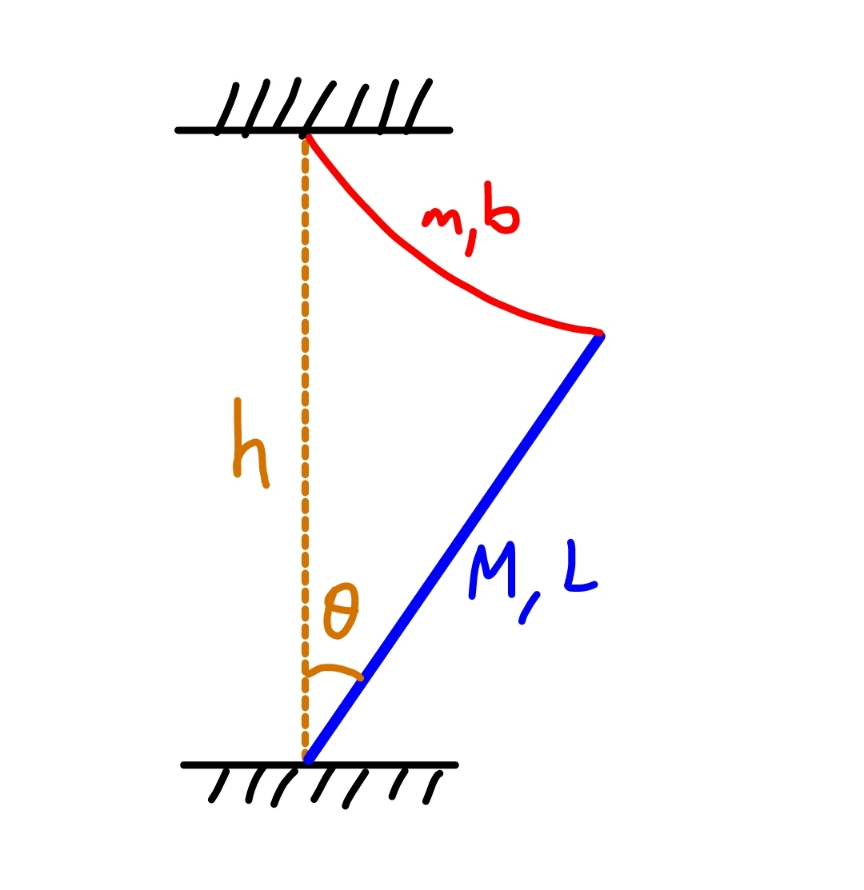
$${a}\:{rope}\:{with}\:{mass}\:{m}\:{and}\:{length}\:{b}\:{is} \\ $$$${connected}\:{on}\:{one}\:{end}\:{with}\:{a}\:{rod}\:{and} \\ $$$${its}\:{other}\:{end}\:{is}\:{fixed}\:{on}\:{the}\:{ceiling} \\ $$$${in}\:{a}\:{height}\:{h}\:{above}\:{the}\:{ground}.\:{the}\: \\ $$$${rod}\:{with}\:{mass}\:{M}\:{and}\:{length}\:{L}\:{is} \\ $$$${connected}\:{through}\:{a}\:{hinge}\:{with}\:{the} \\ $$$${ground}. \\ $$$${find}\:{the}\:{angle}\:\theta. \\ $$$$\left({M}>{m},\:{L}+{b}>{h}\right) \\ $$
Answered by mr W last updated on 12/Oct/22
Commented by Tawa11 last updated on 12/Oct/22
$$\mathrm{Great}\:\mathrm{sir}.\:\mathrm{Weldone}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 14/Oct/22
![ρ=(m/b) let μ=(m/M), η=(h/L), λ=(b/L) Mg((L sin θ)/2)=T_1 L sin ((π/2)−θ+φ) T_1 =((Mg sin θ)/(2 cos (θ−φ))) T_0 =T_1 cos φ a=(T_0 /(ρg))=((Mgb sin θ cos φ)/(2mg cos (θ−φ)))=(b/(2μ((1/(tan θ))+tan φ))) sinh (d_1 /a)=tan φ ⇒(d_1 /a)=sinh^(−1) (tan φ) (h_1 /a)=cosh (d_1 /a)=(√(1+tan^2 φ)) (s_1 /a)=tan φ h_2 =h_1 +h−L cos θ (h_2 /a)=cosh ((d_1 +L sin θ)/a) (h_1 /a)+((h−L cos θ)/a)=cosh ((d_1 +L sin θ)/a) (√(1+tan^2 φ))+((h−L cos θ)/a)=cosh ((d_1 /a)+((L sin θ)/a)) sinh^(−1) (tan φ)+((2μ sin θ)/λ)((1/(tan θ))+tan φ)=cosh^(−1) [(√(1+tan^2 φ))+((2μ(η−cos θ))/λ)((1/(tan θ))+tan φ)] ((s_1 +b)/a)=sinh ((d_1 +L sin θ)/a) ⇒ sinh^(−1) (tan φ)+((2μ sin θ)/λ)((1/(tan θ))+tan φ)=sinh^(−1) [(1+2μ)tan φ+((2μ)/(tan θ))] ⇒ cosh^(−1) [(√(1+tan^2 φ))+((2μ(η−cos θ))/λ)((1/(tan θ))+tan φ)]=sinh^(−1) [(1+2μ)tan φ+((2μ)/(tan θ))]](https://www.tinkutara.com/question/Q178085.png)
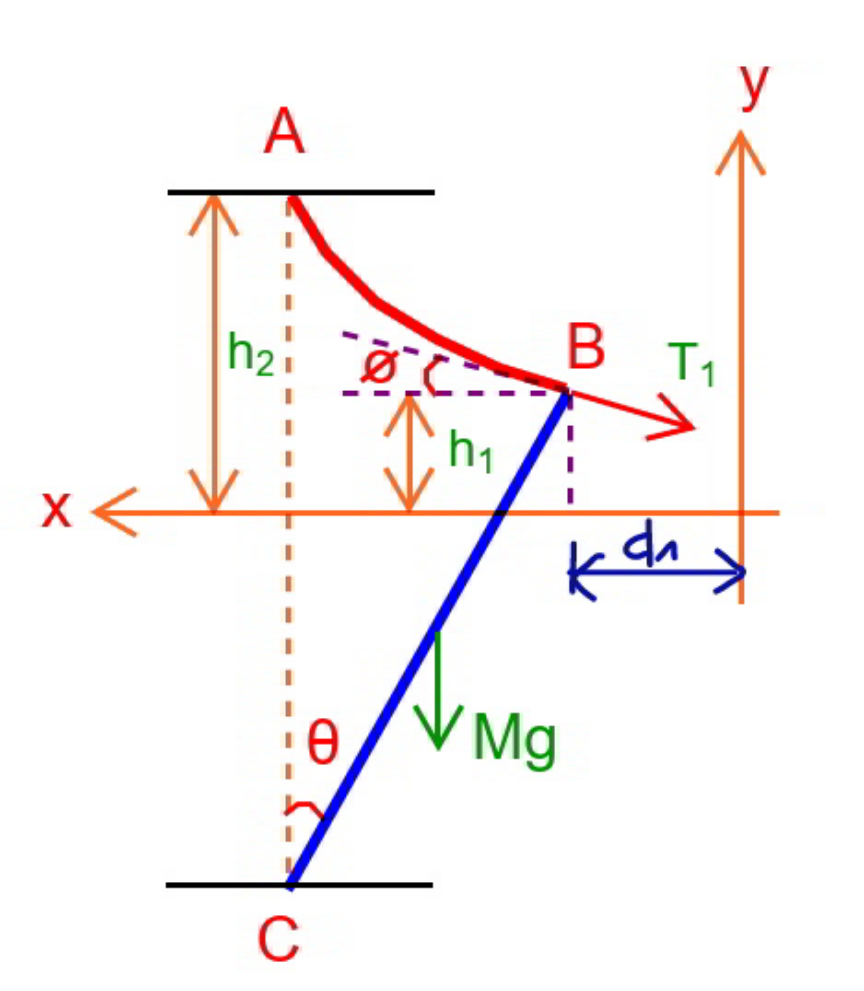
$$\rho=\frac{{m}}{{b}} \\ $$$${let}\:\mu=\frac{{m}}{{M}},\:\eta=\frac{{h}}{{L}},\:\lambda=\frac{{b}}{{L}} \\ $$$${Mg}\frac{{L}\:\mathrm{sin}\:\theta}{\mathrm{2}}={T}_{\mathrm{1}} {L}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta+\phi\right) \\ $$$${T}_{\mathrm{1}} =\frac{{Mg}\:\mathrm{sin}\:\theta}{\mathrm{2}\:\mathrm{cos}\:\left(\theta−\phi\right)} \\ $$$${T}_{\mathrm{0}} ={T}_{\mathrm{1}} \:\mathrm{cos}\:\phi \\ $$$${a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\frac{{Mgb}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\phi}{\mathrm{2}{mg}\:\mathrm{cos}\:\left(\theta−\phi\right)}=\frac{{b}}{\mathrm{2}\mu\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta}+\mathrm{tan}\:\phi\right)} \\ $$$$\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} }{{a}}=\mathrm{tan}\:\phi \\ $$$$\Rightarrow\frac{{d}_{\mathrm{1}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\phi\right) \\ $$$$\frac{{h}_{\mathrm{1}} }{{a}}=\mathrm{cosh}\:\frac{{d}_{\mathrm{1}} }{{a}}=\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\phi} \\ $$$$ \\ $$$$\frac{{s}_{\mathrm{1}} }{{a}}=\mathrm{tan}\:\phi \\ $$$${h}_{\mathrm{2}} ={h}_{\mathrm{1}} +{h}−{L}\:\mathrm{cos}\:\theta \\ $$$$\frac{{h}_{\mathrm{2}} }{{a}}=\mathrm{cosh}\:\frac{{d}_{\mathrm{1}} +{L}\:\mathrm{sin}\:\theta}{{a}} \\ $$$$\frac{{h}_{\mathrm{1}} }{{a}}+\frac{{h}−{L}\:\mathrm{cos}\:\theta}{{a}}=\mathrm{cosh}\:\frac{{d}_{\mathrm{1}} +{L}\:\mathrm{sin}\:\theta}{{a}} \\ $$$$\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\phi}+\frac{{h}−{L}\:\mathrm{cos}\:\theta}{{a}}=\mathrm{cosh}\:\left(\frac{{d}_{\mathrm{1}} }{{a}}+\frac{{L}\:\mathrm{sin}\:\theta}{{a}}\right) \\ $$$$\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\phi\right)+\frac{\mathrm{2}\mu\:\mathrm{sin}\:\theta}{\lambda}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta}+\mathrm{tan}\:\phi\right)=\mathrm{cosh}^{−\mathrm{1}} \:\left[\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\phi}+\frac{\mathrm{2}\mu\left(\eta−\mathrm{cos}\:\theta\right)}{\lambda}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta}+\mathrm{tan}\:\phi\right)\right] \\ $$$$\frac{{s}_{\mathrm{1}} +{b}}{{a}}=\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} +{L}\:\mathrm{sin}\:\theta}{{a}} \\ $$$$\Rightarrow\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\phi\right)+\frac{\mathrm{2}\mu\:\mathrm{sin}\:\theta}{\lambda}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta}+\mathrm{tan}\:\phi\right)=\mathrm{sinh}^{−\mathrm{1}} \:\left[\left(\mathrm{1}+\mathrm{2}\mu\right)\mathrm{tan}\:\phi+\frac{\mathrm{2}\mu}{\mathrm{tan}\:\theta}\right] \\ $$$$\Rightarrow\:\mathrm{cosh}^{−\mathrm{1}} \:\left[\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\phi}+\frac{\mathrm{2}\mu\left(\eta−\mathrm{cos}\:\theta\right)}{\lambda}\left(\frac{\mathrm{1}}{\mathrm{tan}\:\theta}+\mathrm{tan}\:\phi\right)\right]=\mathrm{sinh}^{−\mathrm{1}} \:\left[\left(\mathrm{1}+\mathrm{2}\mu\right)\mathrm{tan}\:\phi+\frac{\mathrm{2}\mu}{\mathrm{tan}\:\theta}\right] \\ $$
