Question-180368

Facebook Tweet Pin

Question Number 180368 by 281981 last updated on 11/Nov/22

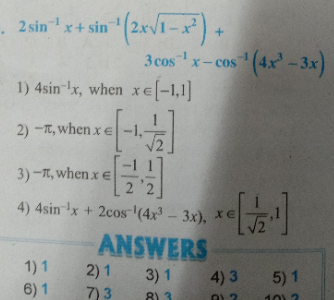
Commented by 281981 last updated on 11/Nov/22

$${ans}:−\pi\:{where}\:{x}\in\left[−\mathrm{1}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right] \\ $$

Commented by mr W last updated on 12/Nov/22

$${can}\:{you}\:{please}\:{show}\:{how}\:{you}\:{get}\:{this} \\ $$$${answer}? \\ $$

Commented by 281981 last updated on 12/Nov/22

i dont know the answer sir,but given answer is option 2

$${i}\:{dont}\:{know}\:{the}\:{answer}\:{sir},{but}\: \\ $$$${given}\:{answer}\:{is}\:{option}\:\mathrm{2} \\ $$

Commented by mr W last updated on 12/Nov/22

then the given answer is wrong. there are multiple right answers. but it can never be −π.

$${then}\:{the}\:{given}\:{answer}\:{is}\:{wrong}. \\ $$$${there}\:{are}\:{multiple}\:{right}\:{answers}. \\ $$$${but}\:{it}\:{can}\:{never}\:{be}\:−\pi. \\ $$

Commented by 281981 last updated on 13/Nov/22

$${ok}\:{sir},{tnq} \\ $$

Answered by Ar Brandon last updated on 11/Nov/22

Let x=sinθ=cos((π/2)−θ) ⇒ 2θ+sin^(−1) (2sinθcosθ)+3((π/2)−θ)−cos^(−1) (cos(3((π/2)−θ))) =2θ+2θ+((3π)/2)−3θ−((3π)/2)+3θ=4θ=4sin^(−1) x, x∈[−1, 1]

$$\mathrm{Let}\:{x}=\mathrm{sin}\theta=\mathrm{cos}\left(\frac{\pi}{\mathrm{2}}−\theta\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{2}\theta+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2sin}\theta\mathrm{cos}\theta\right)+\mathrm{3}\left(\frac{\pi}{\mathrm{2}}−\theta\right)−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{cos}\left(\mathrm{3}\left(\frac{\pi}{\mathrm{2}}−\theta\right)\right)\right) \\ $$$$=\mathrm{2}\theta+\mathrm{2}\theta+\frac{\mathrm{3}\pi}{\mathrm{2}}−\mathrm{3}\theta−\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{3}\theta=\mathrm{4}\theta=\mathrm{4sin}^{−\mathrm{1}} {x},\:{x}\in\left[−\mathrm{1},\:\mathrm{1}\right] \\ $$

Commented by 281981 last updated on 11/Nov/22

$${sir}\:{answer}\:{is}\:{option}\:\mathrm{2} \\ $$

Commented by 281981 last updated on 11/Nov/22

$$−\boldsymbol{\pi}\:{where}\:{x}\in\left[−\mathrm{1}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right] \\ $$

Commented by Ar Brandon last updated on 11/Nov/22

OK let's hope another member propose a solution.

Commented by Acem last updated on 12/Nov/22

$$@\mathrm{281981},\:{well},\:{let}'{s}\:{see}\:{your}\:{solve} \\ $$

Answered by mr W last updated on 12/Nov/22

let t=cos^(−1) x, 0≤t≤π ⇒x=cos t x=cos t=sin ((π/2)−t) ⇒sin^(−1) x=(π/2)−t 2x(√(1−x^2 ))=2 cos t sin t=sin 2t ⇒sin^(−1) (2x(√(1−x^2 )))=2t and 0≤t≤(π/4) 4x^3 −3x=4 cos^3 t−3 cos t=cos 3t ⇒cos^(−1) (4x^3 −3x)=3t and 0≤t≤(π/3) 2 sin^(−1) x+sin^(−1) (2x(√(1−x^2 )))+3 cos^(−1) x−cos^(−1) (4x^3 −3x) =2((π/2)−t)+2t+3t−3t =π with 0≤t≤(π/4), i.e. (1/( (√2)))≤x≤1 or let t=−cos^(−1) x, −π≤t≤0 x=cos (−t)=cos t .....similarly as above 2 sin^(−1) x+sin^(−1) (2x(√(1−x^2 )))+3 cos^(−1) x−cos^(−1) (4x^3 −3x) =2((π/2)−t)+2t−3t+3t =π with −(π/4)≤t≤0, i.e. −1≤x≤−(1/( (√2))) so we get (at least) two possibilities: π with x∈[(1/( (√2))),1] or π with x∈[−1,−(1/( (√2)))]

$${let}\:{t}=\mathrm{cos}^{−\mathrm{1}} {x},\:\mathrm{0}\leqslant{t}\leqslant\pi \\ $$$$\Rightarrow{x}=\mathrm{cos}\:{t} \\ $$$${x}=\mathrm{cos}\:{t}=\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−{t}\right) \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} {x}=\frac{\pi}{\mathrm{2}}−{t} \\ $$$$\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{2}\:\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}=\mathrm{sin}\:\mathrm{2}{t} \\ $$$$\Rightarrow\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)=\mathrm{2}{t}\:{and}\:\mathrm{0}\leqslant{t}\leqslant\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}=\mathrm{4}\:\mathrm{cos}^{\mathrm{3}} \:{t}−\mathrm{3}\:\mathrm{cos}\:{t}=\mathrm{cos}\:\mathrm{3}{t} \\ $$$$\Rightarrow\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}\right)=\mathrm{3}{t}\:{and}\:\mathrm{0}\leqslant{t}\leqslant\frac{\pi}{\mathrm{3}} \\ $$$$\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)+\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} {x}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}\right) \\ $$$$=\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−{t}\right)+\mathrm{2}{t}+\mathrm{3}{t}−\mathrm{3}{t} \\ $$$$=\pi\:{with}\:\mathrm{0}\leqslant{t}\leqslant\frac{\pi}{\mathrm{4}},\:{i}.{e}.\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\leqslant{x}\leqslant\mathrm{1} \\ $$$${or} \\ $$$${let}\:{t}=−\mathrm{cos}^{−\mathrm{1}} {x},\:−\pi\leqslant{t}\leqslant\mathrm{0} \\ $$$${x}=\mathrm{cos}\:\left(−{t}\right)=\mathrm{cos}\:{t} \\ $$$$…..{similarly}\:{as}\:{above} \\ $$$$\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)+\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} {x}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}\right) \\ $$$$=\mathrm{2}\left(\frac{\pi}{\mathrm{2}}−{t}\right)+\mathrm{2}{t}−\mathrm{3}{t}+\mathrm{3}{t} \\ $$$$=\pi\:{with}\:−\frac{\pi}{\mathrm{4}}\leqslant{t}\leqslant\mathrm{0},\:{i}.{e}.\:−\mathrm{1}\leqslant{x}\leqslant−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${so}\:{we}\:{get}\:\left({at}\:{least}\right)\:{two}\:{possibilities}: \\ $$$$\pi\:{with}\:{x}\in\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}},\mathrm{1}\right]\:{or} \\ $$$$\pi\:{with}\:{x}\in\left[−\mathrm{1},−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right] \\ $$

Commented by mr W last updated on 12/Nov/22

check with x=(4/5): 2 sin^(−1) x+sin^(−1) (2x(√(1−x^2 )))+3 cos^(−1) x−cos^(−1) (4x^3 −3x) =2 sin^(−1) (4/5)+sin^(−1) (2×(4/5)(√(1−((4/5))^2 )))+3 cos^(−1) (4/5)−cos^(−1) (4((4/5))^3 −3×((4/5))) =2 sin^(−1) (4/5)+sin^(−1) ((24)/(25))+3 cos^(−1) (4/5)−cos^(−1) (−((44)/(125))) =2 sin^(−1) (4/5)+sin^(−1) ((24)/(25))+3 sin^(−1) (3/5)−(π−cos^(−1) ((44)/(125))) =2 sin^(−1) (4/5)+sin^(−1) ((24)/(25))+3 sin^(−1) (3/5)+cos^(−1) ((44)/(125))−π =π ✓ check with x=−(4/5): 2 sin^(−1) x+sin^(−1) (2x(√(1−x^2 )))+3 cos^(−1) x−cos^(−1) (4x^3 −3x) =2 sin^(−1) (−(4/5))+sin^(−1) (−2×(4/5)(√(1−((4/5))^2 )))+3 cos^(−1) (−(4/5))−cos^(−1) (−4((4/5))^3 +3×((4/5))) =−2 sin^(−1) (4/5)−sin^(−1) ((24)/(25))+3(π−cos^(−1) (4/5))−cos^(−1) ((44)/(125)) =3π−2 sin^(−1) (4/5)−sin^(−1) ((24)/(25))−3 cos^(−1) (4/5)−cos^(−1) ((44)/(125)) =π ✓

$${check}\:{with}\:{x}=\frac{\mathrm{4}}{\mathrm{5}}: \\ $$$$\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)+\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} {x}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}\right) \\ $$$$=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2}×\frac{\mathrm{4}}{\mathrm{5}}\sqrt{\mathrm{1}−\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{2}} }\right)+\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{4}\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{3}} −\mathrm{3}×\left(\frac{\mathrm{4}}{\mathrm{5}}\right)\right) \\ $$$$=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{24}}{\mathrm{25}}+\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{44}}{\mathrm{125}}\right) \\ $$$$=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{24}}{\mathrm{25}}+\mathrm{3}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{5}}−\left(\pi−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{44}}{\mathrm{125}}\right) \\ $$$$=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{24}}{\mathrm{25}}+\mathrm{3}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{5}}+\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{44}}{\mathrm{125}}−\pi \\ $$$$=\pi\:\checkmark \\ $$$${check}\:{with}\:{x}=−\frac{\mathrm{4}}{\mathrm{5}}: \\ $$$$\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} {x}+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)+\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} {x}−\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}\right) \\ $$$$=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \left(−\frac{\mathrm{4}}{\mathrm{5}}\right)+\mathrm{sin}^{−\mathrm{1}} \left(−\mathrm{2}×\frac{\mathrm{4}}{\mathrm{5}}\sqrt{\mathrm{1}−\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{2}} }\right)+\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} \left(−\frac{\mathrm{4}}{\mathrm{5}}\right)−\mathrm{cos}^{−\mathrm{1}} \left(−\mathrm{4}\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{3}} +\mathrm{3}×\left(\frac{\mathrm{4}}{\mathrm{5}}\right)\right) \\ $$$$=−\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{24}}{\mathrm{25}}+\mathrm{3}\left(\pi−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}\right)−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{44}}{\mathrm{125}} \\ $$$$=\mathrm{3}\pi−\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{24}}{\mathrm{25}}−\mathrm{3}\:\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{5}}−\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{44}}{\mathrm{125}} \\ $$$$=\pi\:\checkmark \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply