Question Number 183844 by Michaelfaraday last updated on 30/Dec/22
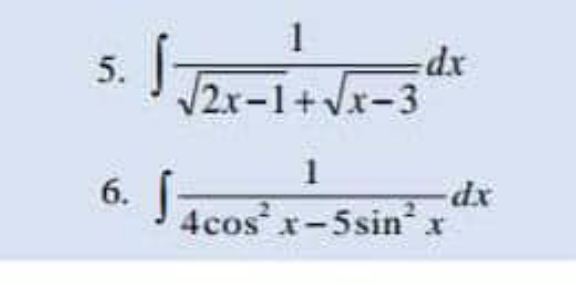
Answered by MJS_new last updated on 31/Dec/22
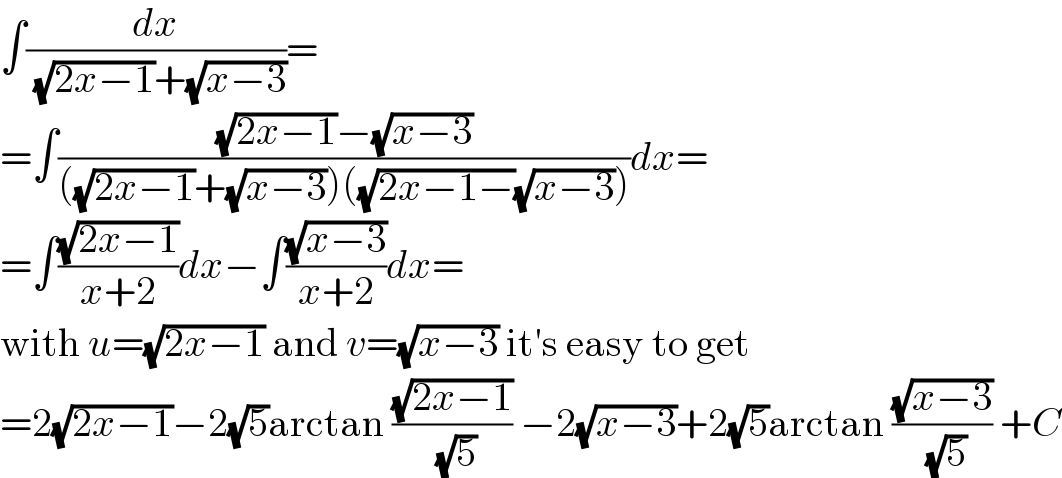
$$\int\frac{{dx}}{\:\sqrt{\mathrm{2}{x}−\mathrm{1}}+\sqrt{{x}−\mathrm{3}}}= \\ $$$$=\int\frac{\sqrt{\mathrm{2}{x}−\mathrm{1}}−\sqrt{{x}−\mathrm{3}}}{\left(\sqrt{\mathrm{2}{x}−\mathrm{1}}+\sqrt{{x}−\mathrm{3}}\right)\left(\sqrt{\mathrm{2}{x}−\mathrm{1}−}\sqrt{{x}−\mathrm{3}}\right)}{dx}= \\ $$$$=\int\frac{\sqrt{\mathrm{2}{x}−\mathrm{1}}}{{x}+\mathrm{2}}{dx}−\int\frac{\sqrt{{x}−\mathrm{3}}}{{x}+\mathrm{2}}{dx}= \\ $$$$\mathrm{with}\:{u}=\sqrt{\mathrm{2}{x}−\mathrm{1}}\:\mathrm{and}\:{v}=\sqrt{{x}−\mathrm{3}}\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{get} \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}{x}−\mathrm{1}}−\mathrm{2}\sqrt{\mathrm{5}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}{x}−\mathrm{1}}}{\:\sqrt{\mathrm{5}}}\:−\mathrm{2}\sqrt{{x}−\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{5}}\mathrm{arctan}\:\frac{\sqrt{{x}−\mathrm{3}}}{\:\sqrt{\mathrm{5}}}\:+{C} \\ $$
Answered by MJS_new last updated on 31/Dec/22
![∫(dx/(4cos^2 x −5sin^2 x))=∫(dx/(4−9sin^2 x))= [t=tan x → dx=(dt/(t^2 +1))] =∫(dt/(4−5t^2 ))=((√5)/(20))ln (((√5)t+2)/( (√5)t−1)) = =((√5)/(20))ln ∣(((√5)sin x +2cos x)/( (√5)sin x −2cos x))∣ +C](https://www.tinkutara.com/question/Q183856.png)
$$\int\frac{{dx}}{\mathrm{4cos}^{\mathrm{2}} \:{x}\:−\mathrm{5sin}^{\mathrm{2}} \:{x}}=\int\frac{{dx}}{\mathrm{4}−\mathrm{9sin}^{\mathrm{2}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\int\frac{{dt}}{\mathrm{4}−\mathrm{5}{t}^{\mathrm{2}} }=\frac{\sqrt{\mathrm{5}}}{\mathrm{20}}\mathrm{ln}\:\frac{\sqrt{\mathrm{5}}{t}+\mathrm{2}}{\:\sqrt{\mathrm{5}}{t}−\mathrm{1}}\:= \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{20}}\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{5}}\mathrm{sin}\:{x}\:+\mathrm{2cos}\:{x}}{\:\sqrt{\mathrm{5}}\mathrm{sin}\:{x}\:−\mathrm{2cos}\:{x}}\mid\:+{C} \\ $$
Commented by Michaelfaraday last updated on 31/Dec/22

$${thanks}\:{sir} \\ $$
