Question Number 185776 by TUN last updated on 27/Jan/23

Answered by MJS_new last updated on 27/Jan/23
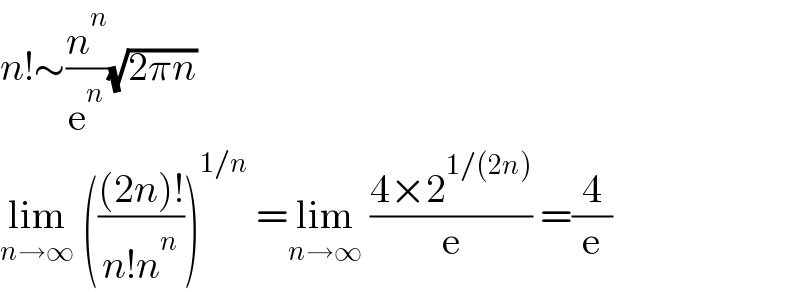
$${n}!\sim\frac{{n}^{{n}} }{\mathrm{e}^{{n}} }\sqrt{\mathrm{2}\pi{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\left(\mathrm{2}{n}\right)!}{{n}!{n}^{{n}} }\right)^{\mathrm{1}/{n}} \:=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{4}×\mathrm{2}^{\mathrm{1}/\left(\mathrm{2}{n}\right)} }{\mathrm{e}}\:=\frac{\mathrm{4}}{\mathrm{e}} \\ $$
Answered by CElcedricjunior last updated on 27/Jan/23
![lim_(n→∞) ((((2n)!)/(n!n^n )))^(1/n) =lim_(n→∞) (((Π_(k=1) ^(2n) k)/(Π_(k=1) ^n k×n^n )))^(1/n) =lim_(n→∞) (((Π_(k=n+1) ^(2n) k)/n^n ))^(1/n) =lim_(n→∞) (Π_(k=n+1) ^(2n) ((k/n)))^(1/n) =>en applicant ln lim_(n→∞) (1/n)ln(Π_(k=n+1) ^(2n) ((k/n))) =lim_(n→∞) (1/n)[ln((1+n)/n)+ln((2+n)/n)+.....ln((2n)/n)] =lim_(n→∞) (1/n)Σ_(k=n+1) ^(2n) ln((k/n)) posons { ((p=k−n−1 pour k=n+1=>p=0)),((pour k=2n =>p=n−1)) :} =lim_(n→∞) (1/n)Σ_(p=0) ^(n−1) ln(((p+n+1)/n)) =lim_(n→∞) (1/n)Σ_(p=1) ^n ln(1+(p/n))=lim_(n→∞) ((b−a)/n)Σ_(p=1) ^n f(a+((b−a)/n)p) avec a=1;b=2;f(x)=ln(x) d′apre^� s notre celebre frere Riemann lim_(n→∞) ln((((2n)!)/(n!n^n )))^(1/n) =∫_1 ^2 lnxdx=[xlnx−x]_1 ^2 lim_(n→∞) ((((2n)!)/(n!n^n )))^(1/n) =e^(2ln2−1) =(4/e) ======================= ...............le celebre cedric junior.......... ================== ==](https://www.tinkutara.com/question/Q185797.png)
$$\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\left(\mathrm{2}\boldsymbol{{n}}\right)!}{\boldsymbol{{n}}!\boldsymbol{{n}}^{\boldsymbol{{n}}} }\right)^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} =\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\mathrm{2}\boldsymbol{{n}}} {\prod}}\boldsymbol{{k}}}{\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\prod}}\boldsymbol{{k}}×\boldsymbol{{n}}^{\boldsymbol{{n}}} }\right)^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} \\ $$$$=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\underset{\boldsymbol{{k}}=\boldsymbol{{n}}+\mathrm{1}} {\overset{\mathrm{2}\boldsymbol{{n}}} {\prod}}\boldsymbol{{k}}}{\boldsymbol{{n}}^{\boldsymbol{{n}}} }\right)^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} =\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left(\underset{\boldsymbol{{k}}=\boldsymbol{{n}}+\mathrm{1}} {\overset{\mathrm{2}\boldsymbol{{n}}} {\prod}}\left(\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}}\right)\right)^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} \\ $$$$=>\boldsymbol{{en}}\:\boldsymbol{{applicant}}\:\boldsymbol{{ln}} \\ $$$$\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{{n}}}\boldsymbol{{ln}}\left(\underset{\boldsymbol{{k}}=\boldsymbol{{n}}+\mathrm{1}} {\overset{\mathrm{2}\boldsymbol{{n}}} {\prod}}\left(\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}}\right)\right) \\ $$$$=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{{n}}}\left[\boldsymbol{{ln}}\frac{\mathrm{1}+{n}}{\boldsymbol{{n}}}+\boldsymbol{{ln}}\frac{\mathrm{2}+{n}}{\boldsymbol{{n}}}+…..\boldsymbol{{ln}}\frac{\mathrm{2}{n}}{\boldsymbol{{n}}}\right] \\ $$$$=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{{n}}}\underset{\boldsymbol{{k}}=\boldsymbol{{n}}+\mathrm{1}} {\overset{\mathrm{2}\boldsymbol{{n}}} {\sum}}\boldsymbol{{ln}}\left(\frac{\boldsymbol{{k}}}{\boldsymbol{{n}}}\right) \\ $$$$\boldsymbol{{posons}}\:\begin{cases}{\boldsymbol{{p}}=\boldsymbol{{k}}−\boldsymbol{{n}}−\mathrm{1}\:\boldsymbol{{pour}}\:\boldsymbol{{k}}=\boldsymbol{{n}}+\mathrm{1}=>\boldsymbol{{p}}=\mathrm{0}}\\{\boldsymbol{{pour}}\:\boldsymbol{{k}}=\mathrm{2}\boldsymbol{{n}}\:=>\boldsymbol{{p}}=\boldsymbol{{n}}−\mathrm{1}}\end{cases} \\ $$$$=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{{n}}}\underset{\boldsymbol{{p}}=\mathrm{0}} {\overset{\boldsymbol{{n}}−\mathrm{1}} {\sum}}\boldsymbol{{ln}}\left(\frac{\boldsymbol{{p}}+\boldsymbol{{n}}+\mathrm{1}}{\boldsymbol{{n}}}\right) \\ $$$$=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\boldsymbol{{n}}}\underset{\boldsymbol{{p}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\boldsymbol{{ln}}\left(\mathrm{1}+\frac{\boldsymbol{{p}}}{\boldsymbol{{n}}}\right)=\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\boldsymbol{{b}}−\boldsymbol{{a}}}{\boldsymbol{{n}}}\underset{\boldsymbol{{p}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\boldsymbol{{f}}\left(\boldsymbol{{a}}+\frac{\boldsymbol{{b}}−\boldsymbol{{a}}}{\boldsymbol{{n}}}\boldsymbol{{p}}\right) \\ $$$$\boldsymbol{{avec}}\:\boldsymbol{{a}}=\mathrm{1};\boldsymbol{{b}}=\mathrm{2};\boldsymbol{{f}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right) \\ $$$$\boldsymbol{{d}}'\boldsymbol{{apr}}\grave {\boldsymbol{{e}s}}\:\boldsymbol{{notre}}\:\boldsymbol{{celebre}}\:\boldsymbol{{frere}}\:\boldsymbol{{Riemann}} \\ $$$$\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\boldsymbol{{ln}}\left(\frac{\left(\mathrm{2}\boldsymbol{{n}}\right)!}{\boldsymbol{{n}}!\boldsymbol{{n}}^{\boldsymbol{{n}}} }\right)^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} =\int_{\mathrm{1}} ^{\mathrm{2}} \boldsymbol{{lnxdx}}=\left[\boldsymbol{{xlnx}}−\boldsymbol{{x}}\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\underset{\boldsymbol{{n}}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\left(\mathrm{2}\boldsymbol{{n}}\right)!}{\boldsymbol{{n}}!\boldsymbol{{n}}^{\boldsymbol{{n}}} }\right)^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} =\boldsymbol{{e}}^{\mathrm{2}\boldsymbol{{ln}}\mathrm{2}−\mathrm{1}} =\frac{\mathrm{4}}{\boldsymbol{{e}}} \\ $$$$======================= \\ $$$$……………{le}\:{celebre}\:{cedric}\:{junior}………. \\ $$$$================== \\ $$$$== \\ $$$$ \\ $$$$ \\ $$
Commented by MJS_new last updated on 27/Jan/23
�� why use 1 line when you can use 10? ��
Commented by CElcedricjunior last updated on 28/Jan/23

$$\blacksquare\blacksquare \\ $$
Answered by qaz last updated on 28/Jan/23
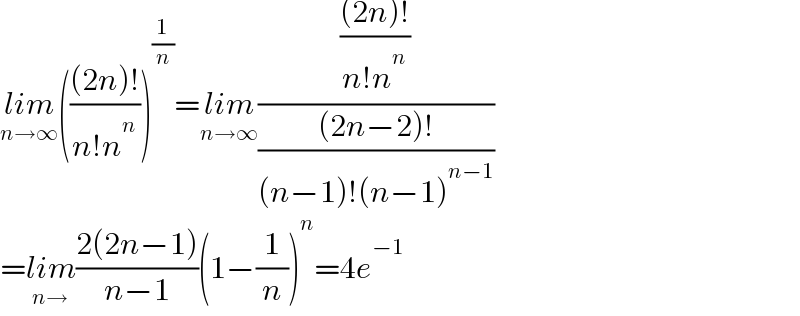
$$\underset{{n}\rightarrow\infty} {{lim}}\left(\frac{\left(\mathrm{2}{n}\right)!}{{n}!{n}^{{n}} }\right)^{\frac{\mathrm{1}}{{n}}} =\underset{{n}\rightarrow\infty} {{lim}}\frac{\frac{\left(\mathrm{2}{n}\right)!}{{n}!{n}^{{n}} }}{\frac{\left(\mathrm{2}{n}−\mathrm{2}\right)!}{\left({n}−\mathrm{1}\right)!\left({n}−\mathrm{1}\right)^{{n}−\mathrm{1}} }} \\ $$$$=\underset{{n}\rightarrow} {{lim}}\frac{\mathrm{2}\left(\mathrm{2}{n}−\mathrm{1}\right)}{{n}−\mathrm{1}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}}\right)^{{n}} =\mathrm{4}{e}^{−\mathrm{1}} \\ $$
