Menu Close

Question-187689

Tinku Tara 0 Comments
Pin




Question Number 187689 by Mingma last updated on 20/Feb/23
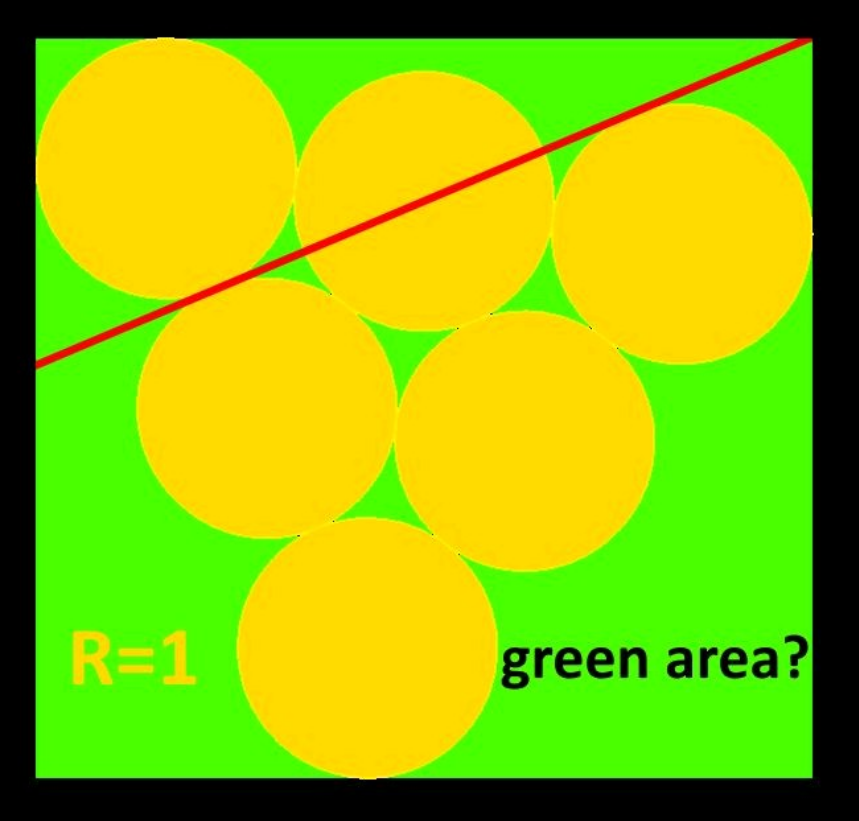
Answered by mr W last updated on 21/Feb/23
Commented by mr W last updated on 26/Feb/23
α=30°−γ 2δ+γ=90° ⇒δ=45°−(γ/2) (1/(tan δ))=1+4 sin α (1/(tan (45°−(γ/2))))=1+4 sin (30°−γ) ((1+tan (γ/2))/(1−tan (γ/2)))=1+2 cos γ−2(√3) sin γ let t=tan (γ/2) ((1+t)/(1−t))=1+((2(1−t^2 ))/(1+t^2 ))−((4(√3)t)/(1−t^2 )) ((1+t)/(1−t))=(((3−t^2 )(1−t^2 )−4(√3)t(1+t^2 ))/((1+t^2 )(1−t^2 ))) (1+t)^2 (1+t^2 )=(3−t^2 )(1−t^2 )−4(√3)t(1+t^2 ) (1+2(√3))t^3 +3t^2 +(1+2(√3))t−1=0 ⇒t≈0.192115=tan (γ/2) (γ≈21.749760°) a=1+4 cos α+1=2+4 cos (30°−γ) (a≈5.958603) β=90°−60°−α=30°−30°+γ=γ b=1+4 cos β+1=2+4 cos γ (b≈5.715244) A_(green) =ab−6×π×1^2 =(2+4 cos (30−γ))(2+4 cos γ)−6π ≈34.054870−6π
$$\alpha=\mathrm{30}°−\gamma \\ $$$$\mathrm{2}\delta+\gamma=\mathrm{90}°\:\Rightarrow\delta=\mathrm{45}°−\frac{\gamma}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\delta}=\mathrm{1}+\mathrm{4}\:\mathrm{sin}\:\alpha \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\left(\mathrm{45}°−\frac{\gamma}{\mathrm{2}}\right)}=\mathrm{1}+\mathrm{4}\:\mathrm{sin}\:\left(\mathrm{30}°−\gamma\right) \\ $$$$\frac{\mathrm{1}+\mathrm{tan}\:\frac{\gamma}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\gamma}{\mathrm{2}}}=\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\gamma−\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\gamma \\ $$$${let}\:{t}=\mathrm{tan}\:\frac{\gamma}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}=\mathrm{1}+\frac{\mathrm{2}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{4}\sqrt{\mathrm{3}}{t}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}=\frac{\left(\mathrm{3}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}^{\mathrm{2}} \right)−\mathrm{4}\sqrt{\mathrm{3}}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$\left(\mathrm{1}+{t}\right)^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)=\left(\mathrm{3}−{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}^{\mathrm{2}} \right)−\mathrm{4}\sqrt{\mathrm{3}}{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right) \\ $$$$\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\right){t}^{\mathrm{3}} +\mathrm{3}{t}^{\mathrm{2}} +\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}\right){t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{t}\approx\mathrm{0}.\mathrm{192115}=\mathrm{tan}\:\frac{\gamma}{\mathrm{2}} \\ $$$$\left(\gamma\approx\mathrm{21}.\mathrm{749760}°\right) \\ $$$$ \\ $$$${a}=\mathrm{1}+\mathrm{4}\:\mathrm{cos}\:\alpha+\mathrm{1}=\mathrm{2}+\mathrm{4}\:\mathrm{cos}\:\left(\mathrm{30}°−\gamma\right) \\ $$$$\left({a}\approx\mathrm{5}.\mathrm{958603}\right) \\ $$$$ \\ $$$$\beta=\mathrm{90}°−\mathrm{60}°−\alpha=\mathrm{30}°−\mathrm{30}°+\gamma=\gamma \\ $$$${b}=\mathrm{1}+\mathrm{4}\:\mathrm{cos}\:\beta+\mathrm{1}=\mathrm{2}+\mathrm{4}\:\mathrm{cos}\:\gamma \\ $$$$\left({b}\approx\mathrm{5}.\mathrm{715244}\right) \\ $$$${A}_{{green}} ={ab}−\mathrm{6}×\pi×\mathrm{1}^{\mathrm{2}} \\ $$$$\:\:\:=\left(\mathrm{2}+\mathrm{4}\:\mathrm{cos}\:\left(\mathrm{30}−\gamma\right)\right)\left(\mathrm{2}+\mathrm{4}\:\mathrm{cos}\:\gamma\right)−\mathrm{6}\pi \\ $$$$\:\:\:\approx\mathrm{34}.\mathrm{054870}−\mathrm{6}\pi \\ $$
Answered by a.lgnaoui last updated on 21/Feb/23
Soit Quadrilatetere[MNPQ] ∡FNQ=((∡YNQ)/2)=(θ/2) tan (θ/2)=((BS)/(NS))=(R/(NS))⇒ NS=(R/(tan (θ/2))) NQ=NS+BK+KT =(R/(tan (θ/2)))+4Rcos (θ/2)+R NQ =cot (θ/2)+4cos (θ/2)+1(1) d autre part MP=NQ MP=IA+AH+HL =R+4Rcos ϕ+R (2) ϕ+∡ACB+((π/2) −(θ/2))=π AB=BC=AC=3R ⇒∡ACB=(π/3) ⇒ϕ=(π/3)+(θ/2) (2) MP=2+4sin ((π/3)+(θ/2)) =2+2sin (θ/2)+2(√3) cos (θ/2) (1)et(2) cot (θ/2)+4cos (θ/2)+1= =2+2sin (θ/2)+2(√3) cos (θ/2) cot (θ/2)=(2(√3) −4)cos (θ/2)+2sin (θ/2)+1 cos (θ/2)=(2(√3) −4)sin (θ/2)cos (θ/2)+2sin^2 (θ/2)+sin (θ/2) cos (θ/2)(1+(4−2(√3) )sin (θ/2))=2sin^2 (θ/2)+sin (θ/2) cos (θ/2)=((2sin^2 (θ/2)+sin (θ/2))/(1+(4−2(√3) )sin (θ/2))) (1−sin^2 (θ/2))=((sin^2 (θ/2)(2sin (θ/2)+1)^2 )/((1+(4−2(√3) )sin (θ/2))^2 )) posons y=sin (θ/2) 1−y^2 =((y^2 (2y+1)^2 )/([1+(4−2(√3) )y]^2 )) 4y^4 +4y^3 +2y^2 =−(4−2(√3) )^2 y^4 −2(4−2(√3) )y^3 +(4−2(√3) )y^2 +2(4−2(√3) )y+1 4(4−(√3) )y^4 +2(3−(√3) )y^3 +((√3) −1)y^2 −2(2−(√3) )y−(1/2)=0 y^4 +(2/(13))(9−(√3) )y^3 +(1/(13))(3(√3)−1 )y^2 −((5−2(√3))/(13))y−((4−(√3))/(26))=0 y=0,48533919 (θ/2)=sin^(−1) (y)≅30° α=∡VNM=30 x=5+1=6 Green Area=x^2 −6𝛑R^2 (R=1) Area( green)=x.z−6πR^2 Area=(PQ×NQ)−6πR^2 z=PQ=PL+TQ+4R[sin (π/6)+cos ((π/6)+(π/3))] PQ=4 Area=x×z=24 Area(green)=24−6π
$${Soit}\:{Quadrilatetere}\left[{MNPQ}\right] \\ $$$$\measuredangle{FNQ}=\frac{\measuredangle{YNQ}}{\mathrm{2}}=\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{{BS}}{{NS}}=\frac{{R}}{{NS}}\Rightarrow\:{NS}=\frac{{R}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\:{NQ}={NS}+{BK}+{KT} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{{R}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}+\mathrm{4}{R}\mathrm{cos}\:\frac{\theta}{\mathrm{2}}+{R} \\ $$$$\:\:\:\:\:\:\:\:{NQ}\:\:=\mathrm{cot}\:\frac{\theta}{\mathrm{2}}+\mathrm{4cos}\:\frac{\theta}{\mathrm{2}}+\mathrm{1}\left(\mathrm{1}\right) \\ $$$${d}\:{autre}\:{part}\:\:{MP}={NQ} \\ $$$${MP}={IA}+{AH}+{HL} \\ $$$$\:\:\:\:\:\:\:\:\:={R}+\mathrm{4}{R}\mathrm{cos}\:\varphi+{R}\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\varphi+\measuredangle{ACB}+\left(\frac{\pi}{\mathrm{2}}\:\:−\frac{\theta}{\mathrm{2}}\right)=\pi \\ $$$${AB}={BC}={AC}=\mathrm{3}{R}\:\Rightarrow\measuredangle{ACB}=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\varphi=\frac{\pi}{\mathrm{3}}+\frac{\theta}{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\:{MP}=\mathrm{2}+\mathrm{4sin}\:\:\left(\frac{\pi}{\mathrm{3}}+\frac{\theta}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}+\mathrm{2sin}\:\frac{\theta}{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{1}\right){et}\left(\mathrm{2}\right)\:\:\:\mathrm{cot}\:\frac{\theta}{\mathrm{2}}+\mathrm{4cos}\:\frac{\theta}{\mathrm{2}}+\mathrm{1}= \\ $$$$\:\:\:\:\:=\mathrm{2}+\mathrm{2sin}\:\frac{\theta}{\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{3}}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}} \\ $$$$\:\:\:\:\:\mathrm{cot}\:\frac{\theta}{\mathrm{2}}=\left(\mathrm{2}\sqrt{\mathrm{3}}\:−\mathrm{4}\right)\mathrm{cos}\:\frac{\theta}{\mathrm{2}}+\mathrm{2sin}\:\frac{\theta}{\mathrm{2}}+\mathrm{1} \\ $$$$\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\left(\mathrm{2}\sqrt{\mathrm{3}}\:−\mathrm{4}\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\mathrm{cos}\:\frac{\theta}{\mathrm{2}}+\mathrm{2sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\left(\mathrm{1}+\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right)=\mathrm{2sin}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{2sin}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}+\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\right)=\frac{\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\left(\mathrm{2sin}\:\frac{\theta}{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)\mathrm{sin}\:\frac{\theta}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${posons}\:\:{y}=\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\mathrm{1}−{y}^{\mathrm{2}} =\frac{{y}^{\mathrm{2}} \left(\mathrm{2}{y}+\mathrm{1}\right)^{\mathrm{2}} }{\left[\mathrm{1}+\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right){y}\right]^{\mathrm{2}} } \\ $$$$\mathrm{4}{y}^{\mathrm{4}} +\mathrm{4}{y}^{\mathrm{3}} +\mathrm{2}{y}^{\mathrm{2}} =−\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}} {y}^{\mathrm{4}} −\mathrm{2}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right){y}^{\mathrm{3}} +\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right){y}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right){y}+\mathrm{1} \\ $$$$\mathrm{4}\left(\mathrm{4}−\sqrt{\mathrm{3}}\:\right){y}^{\mathrm{4}} +\mathrm{2}\left(\mathrm{3}−\sqrt{\mathrm{3}}\:\right){y}^{\mathrm{3}} +\left(\sqrt{\mathrm{3}}\:−\mathrm{1}\right){y}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}−\sqrt{\mathrm{3}}\:\right){y}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{0} \\ $$$$\boldsymbol{{y}}^{\mathrm{4}} +\frac{\mathrm{2}}{\mathrm{13}}\left(\mathrm{9}−\sqrt{\mathrm{3}}\:\right)\boldsymbol{{y}}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{13}}\left(\mathrm{3}\sqrt{\mathrm{3}}−\mathrm{1}\:\right)\boldsymbol{{y}}^{\mathrm{2}} −\frac{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{13}}\boldsymbol{{y}}−\frac{\mathrm{4}−\sqrt{\mathrm{3}}}{\mathrm{26}}=\mathrm{0} \\ $$$${y}=\mathrm{0},\mathrm{48533919} \\ $$$$ \\ $$$$\frac{\theta}{\mathrm{2}}=\mathrm{sin}^{−\mathrm{1}} \left({y}\right)\cong\mathrm{30}°\:\:\alpha=\measuredangle{VNM}=\mathrm{30} \\ $$$$ \\ $$$$\mathrm{x}=\mathrm{5}+\mathrm{1}=\mathrm{6} \\ $$$${Green}\:{Area}=\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{\pi{R}}^{\mathrm{2}} \:\:\:\left({R}=\mathrm{1}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:{Area}\left(\:{green}\right)=\mathrm{x}.\mathrm{z}−\mathrm{6}\pi{R}^{\mathrm{2}} \\ $$$${Area}=\left({PQ}×{NQ}\right)−\mathrm{6}\pi{R}^{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{z}}={PQ}={PL}+{TQ}+\mathrm{4}{R}\left[\mathrm{sin}\:\frac{\pi}{\mathrm{6}}+\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\frac{\pi}{\mathrm{3}}\right)\right] \\ $$$${PQ}=\mathrm{4}\:\:\:\:{Area}=\mathrm{x}×\mathrm{z}=\mathrm{24} \\ $$$$ \\ $$$$\boldsymbol{{Area}}\left({green}\right)=\mathrm{24}−\mathrm{6}\pi \\ $$
Commented by a.lgnaoui last updated on 21/Feb/23
Commented by Rupesh123 last updated on 21/Feb/23
Good job, bro!
Commented by mr W last updated on 22/Feb/23
clearly wrong! PQ=4? how can then three circles be placed side by side? besides clearly PQ>NQ!
$${clearly}\:{wrong}!\: \\ $$$${PQ}=\mathrm{4}?\:{how}\:{can}\:{then}\:{three}\:{circles}\:{be} \\ $$$${placed}\:{side}\:{by}\:{side}? \\ $$$${besides}\:{clearly}\:{PQ}>{NQ}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *