Question Number 25203 by mondodotto@gmail.com last updated on 06/Dec/17
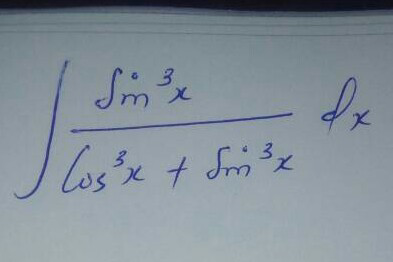
Commented by mondodotto@gmail.com last updated on 07/Dec/17

$$\mathrm{please}\:\mathrm{help} \\ $$
Answered by prakash jain last updated on 07/Dec/17
![∫(1/(1+cot^3 x))dx cot x=u −cosec^2 xdx=du dx=−(du/(1+u^2 )) −∫(du/((1+u^2 )(1+u)(1+u^2 −u))) (1/((1+u^2 )(1+u)(1+u^2 −u))) =((Au+B)/(1+u^2 ))+(C/(1+u))+((Du+E)/(1+u^2 −u)) 1=(Au+B)(1+u)(1+u^2 −u) +C(1+u^2 )(1+u^2 −u)+(Du+E)(1+u^2 )(1+u) =(Au+B)(1+u^3 ) +C(1+2u^2 −u+u^4 −u^3 ) +(Du+E)(1+u+u^2 +u^3 ) =u^4 (A+C+D)+ u^3 (B−C+D+E)+ u^2 (2C+D+E)+ u(A−C+D+E)+ (B+C+E) B+C+E=1 (1) A−C+D+E=0 (2) 2C+D+E=0 (3) B−C+D+E=0 (4) A+C+D=1 (5) (3)−(4) 3C−B=0⇒B=3C (1)−(4) 2C−D=1⇒D=2C−1 (2)−(4) A−B=0⇒A=B=3C from (1) 3C+C+E=1⇒E=1−4C from (5) A+C+D=0 4C+C+2C−1=0⇒C=1/6 A=B=1/2 D=−2/3 E=1/3 ((Au+B)/(1+u^2 ))+(C/(1+u))+((Du+E)/(1+u^2 −u)) =(((u+1))/(2(1+u^2 )))+(1/(6(1+u)))−((2u−1)/(3(1+u^2 −u))) ∫[(((u+1))/(2(1+u^2 )))+(1/(6(1+u)))−((2u−1)/(3(1+u^2 −u)))]du ∫(1/(6(1+u)))du=(1/6)ln (1+u)+C_1 ∫−((2u−1)/(3(1+u^2 −u)))du=−(1/3)ln (1+u^2 −u)+C_2 (1/2)∫((u+1)/(1+u^2 ))=(1/4)∫((2u+1)/(1+u^2 ))du+(1/4)∫(1/(1+u^2 ))du =(1/4)ln (1+u^2 )+(1/4)tan^(−1) u+C_3 substitute u=cot x and add everything and taking care of − sign which was there before partial fractiln ANS=−(1/4)ln (1+cot^2 x)−(1/4)tan^(−1) (cot x) +(1/3)ln (1+cot^2 x−cot x) −(1/6)ln (1+cot x)+C](https://www.tinkutara.com/question/Q25269.png)
$$\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cot}^{\mathrm{3}} {x}}{dx} \\ $$$$\mathrm{cot}\:{x}={u} \\ $$$$−\mathrm{cosec}^{\mathrm{2}} {xdx}={du} \\ $$$${dx}=−\frac{{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$−\int\frac{{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} −{u}\right)} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} −{u}\right)} \\ $$$$=\frac{{Au}+{B}}{\mathrm{1}+{u}^{\mathrm{2}} }+\frac{{C}}{\mathrm{1}+{u}}+\frac{{Du}+{E}}{\mathrm{1}+{u}^{\mathrm{2}} −{u}} \\ $$$$\mathrm{1}=\left({Au}+{B}\right)\left(\mathrm{1}+{u}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} −{u}\right) \\ $$$$+{C}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}^{\mathrm{2}} −{u}\right)+\left({Du}+{E}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+{u}\right) \\ $$$$=\left({Au}+{B}\right)\left(\mathrm{1}+{u}^{\mathrm{3}} \right) \\ $$$$\:\:\:\:+{C}\left(\mathrm{1}+\mathrm{2}{u}^{\mathrm{2}} −{u}+{u}^{\mathrm{4}} −{u}^{\mathrm{3}} \right) \\ $$$$\:\:\:\:\:+\left({Du}+{E}\right)\left(\mathrm{1}+{u}+{u}^{\mathrm{2}} +{u}^{\mathrm{3}} \right) \\ $$$$={u}^{\mathrm{4}} \left({A}+{C}+{D}\right)+ \\ $$$$\:\:\:\:{u}^{\mathrm{3}} \left({B}−{C}+{D}+{E}\right)+ \\ $$$$\:\:\:\:{u}^{\mathrm{2}} \left(\mathrm{2}{C}+{D}+{E}\right)+ \\ $$$$\:\:\:\:{u}\left({A}−{C}+{D}+{E}\right)+ \\ $$$$\:\:\:\:\left({B}+{C}+{E}\right) \\ $$$${B}+{C}+{E}=\mathrm{1}\:\:\:\left(\mathrm{1}\right) \\ $$$${A}−{C}+{D}+{E}=\mathrm{0}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{2}{C}+{D}+{E}=\mathrm{0}\:\left(\mathrm{3}\right) \\ $$$${B}−{C}+{D}+{E}=\mathrm{0}\:\left(\mathrm{4}\right) \\ $$$${A}+{C}+{D}=\mathrm{1}\:\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{3}\right)−\left(\mathrm{4}\right)\:\: \\ $$$$\mathrm{3}{C}−{B}=\mathrm{0}\Rightarrow{B}=\mathrm{3}{C} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{4}\right) \\ $$$$\mathrm{2}{C}−{D}=\mathrm{1}\Rightarrow{D}=\mathrm{2}{C}−\mathrm{1} \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{4}\right) \\ $$$${A}−{B}=\mathrm{0}\Rightarrow{A}={B}=\mathrm{3}{C} \\ $$$${from}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{3}{C}+{C}+{E}=\mathrm{1}\Rightarrow{E}=\mathrm{1}−\mathrm{4}{C} \\ $$$${from}\:\left(\mathrm{5}\right) \\ $$$${A}+{C}+{D}=\mathrm{0} \\ $$$$\mathrm{4}{C}+{C}+\mathrm{2}{C}−\mathrm{1}=\mathrm{0}\Rightarrow{C}=\mathrm{1}/\mathrm{6} \\ $$$${A}={B}=\mathrm{1}/\mathrm{2} \\ $$$${D}=−\mathrm{2}/\mathrm{3} \\ $$$${E}=\mathrm{1}/\mathrm{3} \\ $$$$\frac{{Au}+{B}}{\mathrm{1}+{u}^{\mathrm{2}} }+\frac{{C}}{\mathrm{1}+{u}}+\frac{{Du}+{E}}{\mathrm{1}+{u}^{\mathrm{2}} −{u}} \\ $$$$=\frac{\left({u}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{1}+{u}\right)}−\frac{\mathrm{2}{u}−\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} −{u}\right)} \\ $$$$\int\left[\frac{\left({u}+\mathrm{1}\right)}{\mathrm{2}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}+\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{1}+{u}\right)}−\frac{\mathrm{2}{u}−\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} −{u}\right)}\right]{du} \\ $$$$\int\frac{\mathrm{1}}{\mathrm{6}\left(\mathrm{1}+{u}\right)}{du}=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{1}+{u}\right)+{C}_{\mathrm{1}} \\ $$$$\int−\frac{\mathrm{2}{u}−\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} −{u}\right)}{du}=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left(\mathrm{1}+{u}^{\mathrm{2}} −{u}\right)+{C}_{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{u}+\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{2}{u}+\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}+\frac{\mathrm{1}}{\mathrm{4}}\int\frac{\mathrm{1}}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{1}+{u}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}^{−\mathrm{1}} {u}+{C}_{\mathrm{3}} \\ $$$$\mathrm{substitute}\:{u}=\mathrm{cot}\:{x}\:\mathrm{and}\:\mathrm{add}\:\mathrm{everything} \\ $$$$\mathrm{and}\:\mathrm{taking}\:\mathrm{care}\:\mathrm{of}\:−\:\mathrm{sign}\:\mathrm{which}\:\mathrm{was} \\ $$$$\mathrm{there}\:\mathrm{before}\:\mathrm{partial}\:\mathrm{fractiln} \\ $$$${ANS}=−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{cot}^{\mathrm{2}} {x}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{cot}\:{x}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{cot}^{\mathrm{2}} {x}−\mathrm{cot}\:{x}\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{cot}\:{x}\right)+{C} \\ $$
