Question Number 29201 by mondodotto@gmail.com last updated on 05/Feb/18
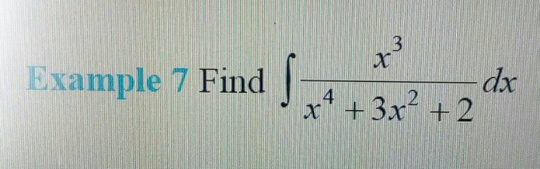
Answered by A1B1C1D1 last updated on 05/Feb/18
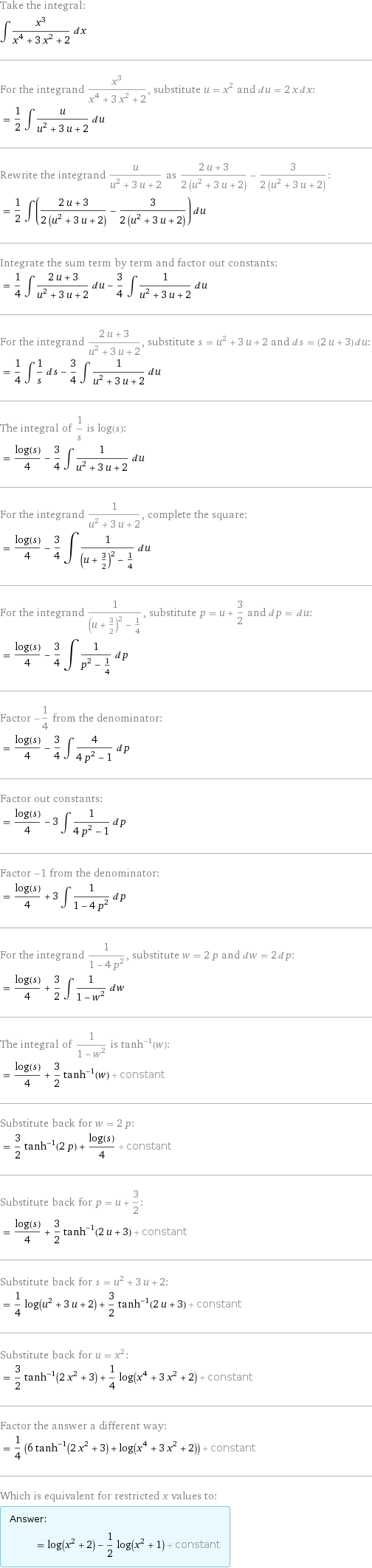
Commented by NECx last updated on 05/Feb/18
$${which}\:{apps}\:{solved}\:{like}\:{this}? \\ $$
Commented by A1B1C1D1 last updated on 05/Feb/18

$$\mathrm{Some},\:\mathrm{such}\:\mathrm{as}\:\mathrm{the}\:\mathrm{Okswthe} \\ $$$$\left.\mathrm{calculator}\:\mathrm{editor}\:\mathrm{and}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{app}\::-\right) \\ $$
Commented by NECx last updated on 05/Feb/18

$${thanks} \\ $$
Commented by Joel578 last updated on 05/Feb/18

$$\mathrm{WolframAlpha} \\ $$
Answered by ajfour last updated on 05/Feb/18
![I=(1/2)∫((x^2 (2xdx))/((x^2 +1)(x^2 +2))) let x^2 =t I= (1/2)∫((tdt)/((t+1)(t+2))) =(1/2)[−∫(dt/(t+1))+2∫(dt/(t+2))] =−(1/2)ln ∣t+1∣+ln ∣t+2∣+c =(1/2)ln [(((x^2 +2)^2 )/(1+x^2 ))] +c .](https://www.tinkutara.com/question/Q29203.png)
$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} \left(\mathrm{2}{xdx}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}\right)} \\ $$$${let}\:{x}^{\mathrm{2}} ={t} \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{tdt}}{\left({t}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[−\int\frac{{dt}}{{t}+\mathrm{1}}+\mathrm{2}\int\frac{{dt}}{{t}+\mathrm{2}}\right] \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mid{t}+\mathrm{1}\mid+\mathrm{ln}\:\mid{t}+\mathrm{2}\mid+{c} \\ $$$$\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left[\frac{\left({x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\right]\:+{c}\:. \\ $$
Commented by NECx last updated on 05/Feb/18
$${so}\:{nice}\:{working}.\boldsymbol{{great}}\:\boldsymbol{{job}}\:\boldsymbol{{sir}}! \\ $$
