Question Number 35703 by scientist last updated on 22/May/18
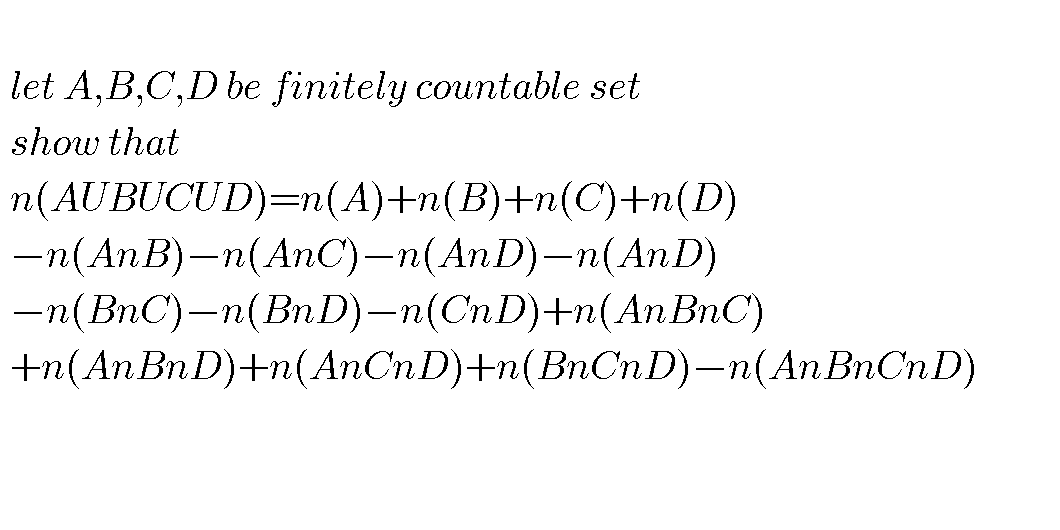
Answered by arcana last updated on 17/Oct/18
![tomando la propiedad de funcion de medida n A,B conjuntos finitos n(A∪B)=n(A)+n(B)−n(A∩B) asi • n((A∪B)∪(C∪D))=n(A∪B)+n(C∪D)−n((A∪B)∩(C∪D)) =[n(A)+n(B)−n(A∩B)]+[n(C)+n(D)−n(C∩D)]−n(((A∪B)∩C)∪((A∪B)∩D)) (/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/) ahora hallamos n([(A∪B)∩C]∪[(A∪B)∩D]) n([(A∪B)∩C]∪[(A∪B)∩D])=n((A∪B)∩C)+ n((A∪B)∩D)−n((A∪B)∩(C∩D)) =[n(A∩C)+n(B∩C)−n(A∩B∩C)]+ [n(A∩D)+n(B∩D)−n(A∩B∩D)]− [n(A∩C∩D)+n(B∩C∩D)−n(A∩B∩C∩D)] (/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/)(/) por lo anterior podemos reescribir • como • n((A∪B)∪(C∪D))=n(A)+n(B)+n(C)+n(D)−n(A∩B)−n(C∩D)− n(A∩C)−n(B∩C)+n(A∩B∩C)]− n(A∩D)−n(B∩D)+n(A∩B∩D)]+ n(A∩C∩D)+n(B∩C∩D)−n(A∩B∩C∩D)](https://www.tinkutara.com/question/Q45889.png)
$$\mathrm{tomando}\:\mathrm{la}\:\mathrm{propiedad}\:\mathrm{de}\:\mathrm{funcion}\:\mathrm{de}\:\mathrm{medida}\:{n} \\ $$$$\mathrm{A},\mathrm{B}\:\mathrm{conjuntos}\:\mathrm{finitos} \\ $$$${n}\left(\mathrm{A}\cup\mathrm{B}\right)={n}\left(\mathrm{A}\right)+{n}\left(\mathrm{B}\right)−{n}\left(\mathrm{A}\cap\mathrm{B}\right) \\ $$$$\mathrm{asi} \\ $$$$\bullet\:{n}\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cup\left(\mathrm{C}\cup\mathrm{D}\right)\right)={n}\left(\mathrm{A}\cup\mathrm{B}\right)+{n}\left(\mathrm{C}\cup\mathrm{D}\right)−{n}\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cap\left(\mathrm{C}\cup\mathrm{D}\right)\right) \\ $$$$=\left[{n}\left(\mathrm{A}\right)+{n}\left(\mathrm{B}\right)−{n}\left(\mathrm{A}\cap\mathrm{B}\right)\right]+\left[{n}\left(\mathrm{C}\right)+{n}\left(\mathrm{D}\right)−{n}\left(\mathrm{C}\cap\mathrm{D}\right)\right]−{n}\left(\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{C}\right)\cup\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{D}\right)\right) \\ $$$$\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{} \\ $$$$\mathrm{ahora}\:\mathrm{hallamos}\:{n}\left(\left[\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{C}\right]\cup\left[\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{D}\right]\right) \\ $$$${n}\left(\left[\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{C}\right]\cup\left[\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{D}\right]\right)={n}\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{C}\right)+ \\ $$$${n}\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cap\mathrm{D}\right)−{n}\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cap\left(\mathrm{C}\cap\mathrm{D}\right)\right) \\ $$$$ \\ $$$$=\left[{n}\left({A}\cap\mathrm{C}\right)+{n}\left(\mathrm{B}\cap\mathrm{C}\right)−{n}\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}\right)\right]+ \\ $$$$\left[{n}\left({A}\cap\mathrm{D}\right)+{n}\left(\mathrm{B}\cap\mathrm{D}\right)−{n}\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{D}\right)\right]− \\ $$$$\left[{n}\left({A}\cap\mathrm{C}\cap\mathrm{D}\right)+{n}\left(\mathrm{B}\cap\mathrm{C}\cap\mathrm{D}\right)−{n}\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}\cap\mathrm{D}\right)\right] \\ $$$$\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{}\frac{}{} \\ $$$$\mathrm{por}\:\mathrm{lo}\:\mathrm{anterior}\:\mathrm{podemos}\:\mathrm{reescribir}\:\bullet\:\mathrm{como} \\ $$$$\bullet\:{n}\left(\left(\mathrm{A}\cup\mathrm{B}\right)\cup\left(\mathrm{C}\cup\mathrm{D}\right)\right)={n}\left(\mathrm{A}\right)+{n}\left(\mathrm{B}\right)+{n}\left(\mathrm{C}\right)+{n}\left(\mathrm{D}\right)−{n}\left({A}\cap\mathrm{B}\right)−{n}\left(\mathrm{C}\cap\mathrm{D}\right)− \\ $$$$\left.{n}\left({A}\cap\mathrm{C}\right)−{n}\left(\mathrm{B}\cap\mathrm{C}\right)+{n}\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}\right)\right]− \\ $$$$\left.{n}\left({A}\cap\mathrm{D}\right)−{n}\left(\mathrm{B}\cap\mathrm{D}\right)+{n}\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{D}\right)\right]+ \\ $$$${n}\left({A}\cap\mathrm{C}\cap\mathrm{D}\right)+{n}\left(\mathrm{B}\cap\mathrm{C}\cap\mathrm{D}\right)−{n}\left(\mathrm{A}\cap\mathrm{B}\cap\mathrm{C}\cap\mathrm{D}\right) \\ $$$$ \\ $$$$ \\ $$
