Question Number 35940 by ajfour last updated on 26/May/18
Commented by ajfour last updated on 26/May/18
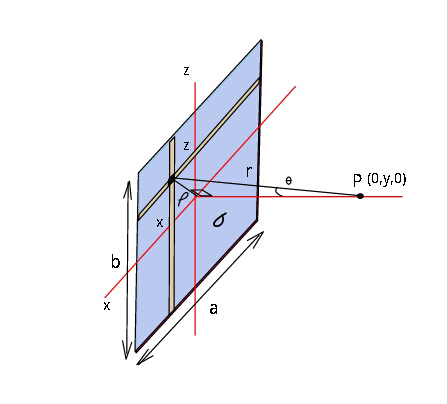
$${Find}\:{electric}\:{field}\:{at}\:\boldsymbol{{P}}\:{due}\:{to}\:{a} \\ $$$${a}\:{charged}\:{rectangular}\:{plate}\:{of} \\ $$$${surface}\:{charge}\:{density}\:\boldsymbol{\sigma}. \\ $$
Answered by ajfour last updated on 26/May/18
![dEcos ΞΈ=((Οydxdy)/(4ΟΞ΅_0 r^3 )) E_P =((Οy)/(4ΟΞ΅_0 ))β«_(β(a/2)) ^( (a/2)) [β«_(β(b/2)) ^( (b/2)) (dz/((x^2 +y^2 +z^2 )^(3/2) ))]dx let z=(β(x^2 +y^2 )) tan Ο E_P =((Οy)/(4ΟΞ΅_0 ))β«_(β(a/2)) ^( (a/2)) [β«_(βΟ_0 ) ^( Ο_0 ) (((β(x^2 +y^2 )) sec^2 ΟdΟ)/( (β(x^2 +y^2 )) (x^2 +y^2 )sec^3 Ο))]dx E_P =((Οy)/(4ΟΞ΅_0 ))β«_(β(a/2)) ^( (a/2)) ((2sin Ο_0 )/(x^2 +y^2 )) dx E_P =((Οy)/(4ΟΞ΅_0 ))β«_(β(a/2)) ^( (a/2)) (b/((x^2 +y^2 )(β(x^2 +y^2 +(b^2 /4))))) dx now let (β(x^2 +y^2 )) =(b/2)cot Ο ; β 2xdx=(b^2 /4)(2cot Ο)(βcosec^2 Ο)dΟ E_P =((2Οyb)/(4ΟΞ΅_0 ))β«_Ο_0 ^( Ο_1 ) ((β(b^2 /4)cosec^3 Ο cos Ο dΟ)/(x((b^2 /4)cot^2 Ο)((b/2)cosec Ο))) dx E_P =β((Οy)/(ΟΞ΅_0 ))β«_Ο_0 ^( Ο_1 ) ((sec Ο)/( (β((b^2 /4)cot^2 Οβy^2 ))))dΟ As cot Ο_1 =((β((a^2 /4)+y^2 ))/(b/2)) ; cot Ο_0 =(y/(b/2)) β E_P =((Οy)/(ΟΞ΅_0 ))β«_Ο_1 ^( Ο_0 ) ((sec Οtan Ο)/( (β((b^2 /4)βy^2 tan^2 Ο)))) dΟ let sec Ο = t E_P =(Ο/(ΟΞ΅_0 ))β«_Ο_1 ^( Ο_0 ) ((d(ysec Ο))/( (β((b^2 /4)+y^2 βy^2 sec^2 Ο)))) E_P =(Ο/(ΟΞ΅_0 ))sin^(β1) (((ysec Ο)/( (β((b^2 /4)+y^2 )))))β£_Ο_1 ^Ο_0 E_P =(Ο/(ΟΞ΅_0 ))[sin^(β1) (cos Ο_0 sec Ο_0 )βsin^(β1) ( (y/( (β((b^2 /4)+y^2 )))).((β((a^2 /4)+(b^2 /4)+y^2 ))/( (β((a^2 /4)+y^2 )))))] E_P =(Ο/(2Ξ΅_0 ))[1β(2/Ο)sin^(β1) ( (y/( (β((b^2 /4)+y^2 )))).((β((a^2 /4)+(b^2 /4)+y^2 ))/( (β((a^2 /4)+y^2 )))))] β (correct eventually, thanks to tanmay sir).](https://www.tinkutara.com/question/Q35945.png)
$${dE}\mathrm{cos}\:\theta=\frac{\sigma{ydxdy}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} {r}^{\mathrm{3}} } \\ $$$${E}_{{P}} =\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{β\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \left[\int_{β\frac{{b}}{\mathrm{2}}} ^{\:\:\frac{{b}}{\mathrm{2}}} \frac{{dz}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\right]{dx} \\ $$$$\:\:\:\:{let}\:{z}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\mathrm{tan}\:\phi \\ $$$${E}_{{P}} =\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{β\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \left[\int_{β\phi_{\mathrm{0}} } ^{\:\:\phi_{\mathrm{0}} } \frac{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\mathrm{sec}\:^{\mathrm{2}} \phi{d}\phi}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\mathrm{sec}\:^{\mathrm{3}} \phi}\right]{dx} \\ $$$${E}_{{P}} =\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{β\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \frac{\mathrm{2sin}\:\phi_{\mathrm{0}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:{dx} \\ $$$${E}_{{P}} =\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{β\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \frac{{b}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}\:{dx} \\ $$$$\:\:\:{now}\:\:{let}\:\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\frac{{b}}{\mathrm{2}}\mathrm{cot}\:\psi\:\:;\:\Rightarrow \\ $$$$\mathrm{2}{xdx}=\frac{{b}^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{2cot}\:\psi\right)\left(β\mathrm{cosec}\:^{\mathrm{2}} \psi\right){d}\psi \\ $$$${E}_{{P}} =\frac{\mathrm{2}\sigma{yb}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{\psi_{\mathrm{0}} } ^{\:\:\psi_{\mathrm{1}} } \frac{β\frac{{b}^{\mathrm{2}} }{\mathrm{4}}\mathrm{cosec}\:^{\mathrm{3}} \psi\:\mathrm{cos}\:\psi\:{d}\psi}{{x}\left(\frac{{b}^{\mathrm{2}} }{\mathrm{4}}\mathrm{cot}\:^{\mathrm{2}} \psi\right)\left(\frac{{b}}{\mathrm{2}}\mathrm{cosec}\:\psi\right)}\:{dx} \\ $$$$\:\:\:\:{E}_{{P}} \:=β\frac{\sigma{y}}{\pi\epsilon_{\mathrm{0}} }\int_{\psi_{\mathrm{0}} } ^{\:\:\psi_{\mathrm{1}} } \frac{\mathrm{sec}\:\psi}{\:\sqrt{\frac{{b}^{\mathrm{2}} }{\mathrm{4}}\mathrm{cot}\:^{\mathrm{2}} \psiβ{y}^{\mathrm{2}} }}{d}\psi \\ $$$${As}\:\:\mathrm{cot}\:\psi_{\mathrm{1}} =\frac{\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} }}{{b}/\mathrm{2}}\:;\:\mathrm{cot}\:\psi_{\mathrm{0}} =\frac{{y}}{{b}/\mathrm{2}} \\ $$$$\Rightarrow\:{E}_{{P}} =\frac{\sigma{y}}{\pi\epsilon_{\mathrm{0}} }\int_{\psi_{\mathrm{1}} } ^{\:\:\psi_{\mathrm{0}} } \frac{\mathrm{sec}\:\psi\mathrm{tan}\:\psi}{\:\sqrt{\frac{{b}^{\mathrm{2}} }{\mathrm{4}}β{y}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \psi}}\:{d}\psi \\ $$$${let}\:\:\mathrm{sec}\:\psi\:=\:{t} \\ $$$${E}_{{P}} =\frac{\sigma}{\pi\epsilon_{\mathrm{0}} }\int_{\psi_{\mathrm{1}} } ^{\:\:\psi_{\mathrm{0}} } \frac{{d}\left({y}\mathrm{sec}\:\psi\right)}{\:\sqrt{\frac{{b}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} β{y}^{\mathrm{2}} \mathrm{sec}\:^{\mathrm{2}} \psi}} \\ $$$${E}_{{P}} =\frac{\sigma}{\pi\epsilon_{\mathrm{0}} }\mathrm{sin}^{β\mathrm{1}} \left(\frac{{y}\mathrm{sec}\:\psi}{\:\sqrt{\frac{{b}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} }}\right)\mid_{\psi_{\mathrm{1}} } ^{\psi_{\mathrm{0}} } \\ $$$${E}_{{P}} =\frac{\sigma}{\pi\epsilon_{\mathrm{0}} }\left[\mathrm{sin}^{β\mathrm{1}} \left(\mathrm{cos}\:\psi_{\mathrm{0}} \mathrm{sec}\:\psi_{\mathrm{0}} \right)β\mathrm{sin}^{β\mathrm{1}} \left(\:\frac{{y}}{\:\sqrt{\frac{{b}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} }}.\frac{\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{{b}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} }}{\:\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} }}\right)\right] \\ $$$${E}_{{P}} =\frac{\sigma}{\mathrm{2}\epsilon_{\mathrm{0}} }\left[\mathrm{1}β\frac{\mathrm{2}}{\pi}\mathrm{sin}^{β\mathrm{1}} \left(\:\frac{{y}}{\:\sqrt{\frac{{b}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} }}.\frac{\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+\frac{{b}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} }}{\:\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} }}\right)\right] \\ $$$$\:\blacksquare\:\:\:\left({correct}\:{eventually},\:{thanks}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:{to}\:{tanmay}\:{sir}\right). \\ $$