Menu Close

Question-37989

Tinku Tara 0 Comments
Pin




Question Number 37989 by ajfour last updated on 20/Jun/18
Commented by ajfour last updated on 20/Jun/18
(i)Find area of blue square and red square. (ii)Find θ for which corners of red square lies on sides of blue square.
$$\left({i}\right){Find}\:{area}\:{of}\:{blue}\:{square}\:{and}\: \\ $$$${red}\:{square}. \\ $$$$\left({ii}\right){Find}\:\theta\:{for}\:{which}\:{corners}\:{of} \\ $$$${red}\:{square}\:{lies}\:{on}\:{sides}\:{of}\:{blue} \\ $$$${square}. \\ $$
Commented by MrW3 last updated on 20/Jun/18
(i) side length of blue square: a_1 =(a/(cos θ))−a sin θ (1+tan θ) ⇒a_1 =a (cos θ−sin θ) ⇒A_1 =a_1 ^2 =a^2 (1−sin 2θ) side length of red square: a_2 =a tan θ sin α with tan α=(a/(a−a tan θ))=((cos θ)/(cos θ−sin θ)) or sin α=((cos θ)/( (√(1+cos^2 θ−sin 2θ)))) ⇒a_2 =a ((sin θ)/( (√(1+cos^2 θ−sin 2θ)))) ⇒A_2 =a_2 ^2 =a^2 ((sin^2 θ)/(1+cos^2 θ−sin 2θ)) (ii) a_1 =a_2 [sin (α−θ)+cos (α−θ)] a_1 =a_2 [sin α (sin θ+cos θ)+cos α (cos θ−sin θ)] (cos θ−sin θ)=((sin θ)/( (√(1+cos^2 θ−sin 2θ))))[((cos θ (sin θ+cos θ))/( (√(1+cos^2 θ−sin 2θ)))) +(((cos θ−sin θ)^2 )/( (√(1+cos^2 θ−sin 2θ))))] cos θ−sin θ=((sin θ (sin θ cos θ+cos^2 θ+1−sin 2θ))/(1+cos^2 θ−sin 2θ)) cos θ−sin θ=((sin^2 θ cos θ)/(1+cos^2 θ−sin 2θ))+sin θ 2(cos θ−2sin θ)=((sin θ sin 2θ)/(1+cos^2 θ−sin 2θ)) 2(cos θ−2sin θ)(1+cos^2 θ+sin 2θ)=sin θ sin 2θ ⇒θ≈23.3°
$$\left({i}\right) \\ $$$${side}\:{length}\:{of}\:{blue}\:{square}: \\ $$$${a}_{\mathrm{1}} =\frac{{a}}{\mathrm{cos}\:\theta}−{a}\:\mathrm{sin}\:\theta\:\left(\mathrm{1}+\mathrm{tan}\:\theta\right) \\ $$$$\Rightarrow{a}_{\mathrm{1}} ={a}\:\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right) \\ $$$$\Rightarrow{A}_{\mathrm{1}} ={a}_{\mathrm{1}} ^{\mathrm{2}} ={a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$ \\ $$$${side}\:{length}\:{of}\:{red}\:{square}: \\ $$$${a}_{\mathrm{2}} ={a}\:\mathrm{tan}\:\theta\:\mathrm{sin}\:\alpha\:{with} \\ $$$$\mathrm{tan}\:\alpha=\frac{{a}}{{a}−{a}\:\mathrm{tan}\:\theta}=\frac{\mathrm{cos}\:\theta}{\mathrm{cos}\:\theta−\mathrm{sin}\:\theta} \\ $$$${or}\:\mathrm{sin}\:\alpha=\frac{\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta}} \\ $$$$\Rightarrow{a}_{\mathrm{2}} ={a}\:\frac{\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta}} \\ $$$$\Rightarrow{A}_{\mathrm{2}} ={a}_{\mathrm{2}} ^{\mathrm{2}} ={a}^{\mathrm{2}} \frac{\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$ \\ $$$$\left({ii}\right) \\ $$$${a}_{\mathrm{1}} ={a}_{\mathrm{2}} \left[\mathrm{sin}\:\left(\alpha−\theta\right)+\mathrm{cos}\:\left(\alpha−\theta\right)\right] \\ $$$${a}_{\mathrm{1}} ={a}_{\mathrm{2}} \left[\mathrm{sin}\:\alpha\:\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)+\mathrm{cos}\:\alpha\:\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)\right] \\ $$$$\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)=\frac{\mathrm{sin}\:\theta}{\:\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta}}\left[\frac{\mathrm{cos}\:\theta\:\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)}{\:\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta}}\:+\frac{\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{\:\sqrt{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta}}\right] \\ $$$$\mathrm{cos}\:\theta−\mathrm{sin}\:\theta=\frac{\mathrm{sin}\:\theta\:\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta+\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{1}−\mathrm{sin}\:\mathrm{2}\theta\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\mathrm{cos}\:\theta−\mathrm{sin}\:\theta=\frac{\mathrm{sin}^{\mathrm{2}} \:\theta\:\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta}+\mathrm{sin}\:\theta \\ $$$$\mathrm{2}\left(\mathrm{cos}\:\theta−\mathrm{2sin}\:\theta\right)=\frac{\mathrm{sin}\:\theta\:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\mathrm{2}\left(\mathrm{cos}\:\theta−\mathrm{2sin}\:\theta\right)\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\theta+\mathrm{sin}\:\mathrm{2}\theta\right)=\mathrm{sin}\:\theta\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$ \\ $$$$\Rightarrow\theta\approx\mathrm{23}.\mathrm{3}° \\ $$
Commented by ajfour last updated on 20/Jun/18
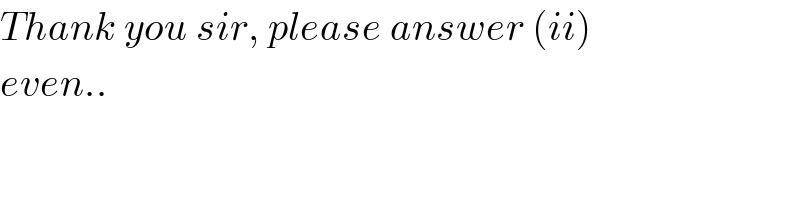
Thank you sir, please answer (ii) even..
$${Thank}\:{you}\:{sir},\:{please}\:{answer}\:\left({ii}\right) \\ $$$${even}.. \\ $$
Commented by MrW3 last updated on 20/Jun/18
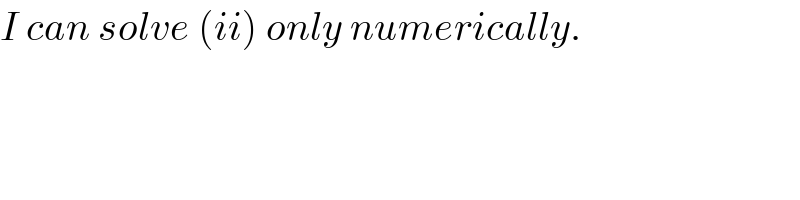
I can solve (ii) only numerically.
$${I}\:{can}\:{solve}\:\left({ii}\right)\:{only}\:{numerically}. \\ $$
Commented by ajfour last updated on 20/Jun/18
yes Sir, this is right. Thank You.
$${yes}\:{Sir},\:{this}\:{is}\:{right}.\:{Thank}\:{You}. \\ $$
Commented by MrW3 last updated on 20/Jun/18
see correction. θ≈23.3°.
$${see}\:{correction}.\:\theta\approx\mathrm{23}.\mathrm{3}°. \\ $$
Commented by MrW3 last updated on 20/Jun/18
Answered by ajfour last updated on 20/Jun/18
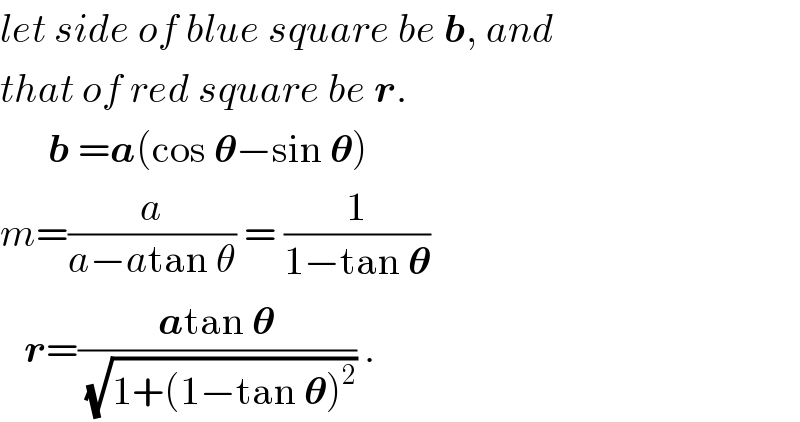
let side of blue square be b, and that of red square be r. b =a(cos 𝛉−sin 𝛉) m=(a/(a−atan θ)) = (1/(1−tan 𝛉)) r=((atan 𝛉)/( (√(1+(1−tan 𝛉)^2 )))) .
$${let}\:{side}\:{of}\:{blue}\:{square}\:{be}\:\boldsymbol{{b}},\:{and} \\ $$$${that}\:{of}\:{red}\:{square}\:{be}\:\boldsymbol{{r}}. \\ $$$$\:\:\:\:\:\:\boldsymbol{{b}}\:=\boldsymbol{{a}}\left(\mathrm{cos}\:\boldsymbol{\theta}−\mathrm{sin}\:\boldsymbol{\theta}\right) \\ $$$${m}=\frac{{a}}{{a}−{a}\mathrm{tan}\:\theta}\:=\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:\boldsymbol{\theta}} \\ $$$$\:\:\:\boldsymbol{{r}}=\frac{\boldsymbol{{a}}\mathrm{tan}\:\boldsymbol{\theta}}{\:\sqrt{\mathrm{1}+\left(\mathrm{1}−\mathrm{tan}\:\boldsymbol{\theta}\right)^{\mathrm{2}} }}\:. \\ $$
Answered by ajfour last updated on 20/Jun/18
let bottom corner of red square be B(h,k) and m=(a/(a−atan θ)) ⇒ 1+mtan θ = m (k/(h−atan θ)) = m (i) (k/(a−h)) = (1/m) ....(ii) if B lies on lower side of blue square , then k= htan θ ...(iii) from (ii) and (iii): mhtan θ=a−h ⇒ h = (a/(1+mtan θ)) ; k=((atan θ)/(1+mtan θ)) since 1+mtan θ = m h=(a/m) ; k = ((atan 𝛉)/m) Using in (i): ((atan θ)/m)= a−amtan θ tan θ=m−m^2 tan θ tan θ=((1−((tan θ)/((1−tan θ))))/(1−tan θ)) let tan θ = s ⇒ s(1−s)^2 = 1−2s θ = tan^(−1) s . (In good agreement with your answer, Sir ).
$${let}\:{bottom}\:{corner}\:{of}\:{red}\:{square} \\ $$$${be}\:{B}\left({h},{k}\right)\:\:{and}\:\:\:{m}=\frac{{a}}{{a}−{a}\mathrm{tan}\:\theta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\mathrm{1}+{m}\mathrm{tan}\:\theta\:=\:{m} \\ $$$$\:\:\:\:\:\:\frac{{k}}{{h}−{a}\mathrm{tan}\:\theta}\:=\:{m}\:\:\:\:\left({i}\right) \\ $$$$\:\:\:\frac{{k}}{{a}−{h}}\:=\:\frac{\mathrm{1}}{{m}}\:\:\:\:….\left({ii}\right) \\ $$$${if}\:{B}\:{lies}\:{on}\:{lower}\:{side}\:{of}\:{blue} \\ $$$${square}\:,\:{then}\:\:\:{k}=\:{h}\mathrm{tan}\:\theta\:\:\:…\left({iii}\right) \\ $$$${from}\:\left({ii}\right)\:{and}\:\left({iii}\right): \\ $$$$\:\:{mh}\mathrm{tan}\:\theta={a}−{h} \\ $$$$\Rightarrow\:\:\:\:\:{h}\:=\:\frac{{a}}{\mathrm{1}+{m}\mathrm{tan}\:\theta}\:;\:{k}=\frac{{a}\mathrm{tan}\:\theta}{\mathrm{1}+{m}\mathrm{tan}\:\theta} \\ $$$${since}\:\mathrm{1}+{m}\mathrm{tan}\:\theta\:=\:{m} \\ $$$$\:\:\:\:\boldsymbol{{h}}=\frac{\boldsymbol{{a}}}{\boldsymbol{{m}}}\:;\:\:\:\boldsymbol{{k}}\:=\:\frac{\boldsymbol{{a}}\mathrm{tan}\:\boldsymbol{\theta}}{\boldsymbol{{m}}} \\ $$$${Using}\:{in}\:\left({i}\right): \\ $$$$\:\:\:\:\:\:\:\frac{{a}\mathrm{tan}\:\theta}{{m}}=\:{a}−{am}\mathrm{tan}\:\theta \\ $$$$\:\:\:\:\:\mathrm{tan}\:\theta={m}−{m}^{\mathrm{2}} \mathrm{tan}\:\theta \\ $$$$\:\:\:\:\:\mathrm{tan}\:\theta=\frac{\mathrm{1}−\frac{\mathrm{tan}\:\theta}{\left(\mathrm{1}−\mathrm{tan}\:\theta\right)}}{\mathrm{1}−\mathrm{tan}\:\theta} \\ $$$${let}\:\:\mathrm{tan}\:\theta\:=\:{s} \\ $$$$\:\:\:\Rightarrow\:\:\:\:\:{s}\left(\mathrm{1}−{s}\right)^{\mathrm{2}} \:=\:\mathrm{1}−\mathrm{2}{s} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\theta\:=\:\mathrm{tan}^{−\mathrm{1}} \:{s}\:. \\ $$$$\:\:\:\left({In}\:{good}\:{agreement}\:{with}\:{your}\right. \\ $$$$\left.\:\:\:\:\:\:\:{answer},\:{Sir}\:\right). \\ $$
Commented by MrW3 last updated on 20/Jun/18
��

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *