Question Number 39381 by rahul 19 last updated on 05/Jul/18

Answered by ajfour last updated on 06/Jul/18
![f ′(x)≥[f(x)]^3 +[f(x)]^(−1) and f(0)=1 , f(a)=3^(1/4) ⇒ ∫_1 ^( y) (dy/(y^3 +(1/y))) ≥ ∫_0 ^( x) dx ⇒ (1/2)∫_1 ^( y) ((2ydy)/(y^4 +1)) ≥ x or tan^(−1) y^2 −tan^(−1) 1 ≥ 2x for x=a , y^2 = (√3) ⇒ 2a ≤ (π/3)−(π/4) ((216a)/π) ≤ 9 .](https://www.tinkutara.com/question/Q39393.png)
$${f}\:'\left({x}\right)\geqslant\left[{f}\left({x}\right)\right]^{\mathrm{3}} +\left[{f}\left({x}\right)\right]^{−\mathrm{1}} \\ $$$${and}\:{f}\left(\mathrm{0}\right)=\mathrm{1}\:,\:\:{f}\left({a}\right)=\mathrm{3}^{\mathrm{1}/\mathrm{4}} \\ $$$$\Rightarrow\:\:\:\int_{\mathrm{1}} ^{\:\:{y}} \frac{{dy}}{{y}^{\mathrm{3}} +\frac{\mathrm{1}}{{y}}}\:\geqslant\:\int_{\mathrm{0}} ^{\:\:{x}} {dx} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\:\:{y}} \:\frac{\mathrm{2}{ydy}}{{y}^{\mathrm{4}} +\mathrm{1}}\:\geqslant\:{x} \\ $$$${or}\:\:\:\:\mathrm{tan}^{−\mathrm{1}} {y}^{\mathrm{2}} −\mathrm{tan}^{−\mathrm{1}} \mathrm{1}\:\geqslant\:\mathrm{2}{x} \\ $$$$\:\:\:\:\:\:{for}\:{x}={a}\:,\:{y}^{\mathrm{2}} =\:\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{2}{a}\:\leqslant\:\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{4}}\: \\ $$$$\:\:\:\:\:\:\frac{\mathrm{216}{a}}{\pi}\:\leqslant\:\mathrm{9}\:. \\ $$
Commented by rahul 19 last updated on 06/Jul/18
from where dx come ?
why it's less than than dy wala integral (Step 1)
Commented by ajfour last updated on 06/Jul/18
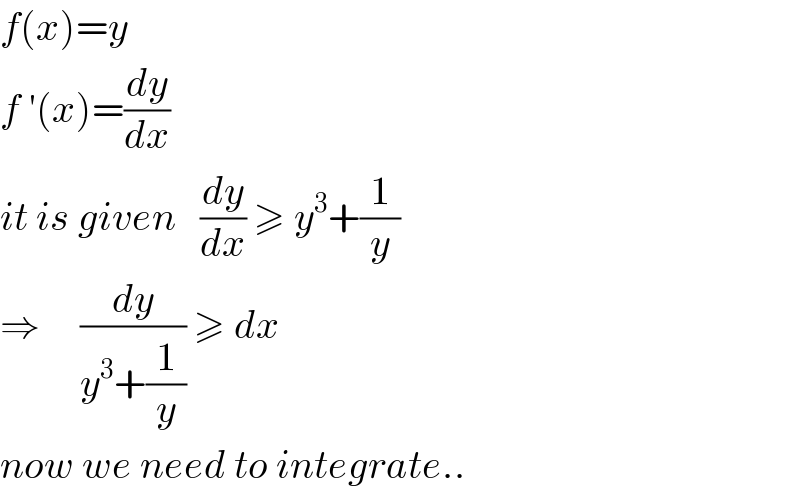
$${f}\left({x}\right)={y} \\ $$$${f}\:'\left({x}\right)=\frac{{dy}}{{dx}} \\ $$$${it}\:{is}\:{given}\:\:\:\frac{{dy}}{{dx}}\:\geqslant\:{y}^{\mathrm{3}} +\frac{\mathrm{1}}{{y}} \\ $$$$\Rightarrow\:\:\:\:\:\frac{{dy}}{{y}^{\mathrm{3}} +\frac{\mathrm{1}}{{y}}}\:\geqslant\:{dx}\:\: \\ $$$${now}\:{we}\:{need}\:{to}\:{integrate}.. \\ $$
Commented by rahul 19 last updated on 06/Jul/18
Thank you Sir ! ��������
