Question Number 45082 by ajfour last updated on 08/Oct/18
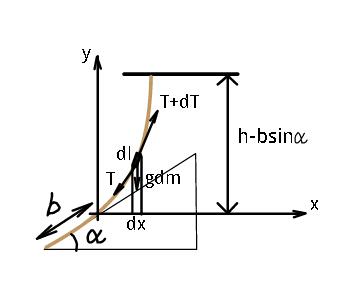
Commented by ajfour last updated on 08/Oct/18
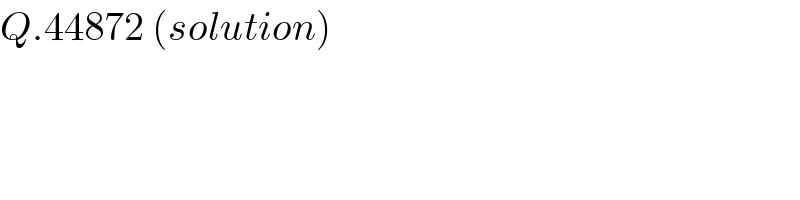
$${Q}.\mathrm{44872}\:\left({solution}\right) \\ $$
Answered by ajfour last updated on 09/Oct/18
![Tcos θdθ+dTsin θ = λg(dx)sec θ ..(i) dTcos θ = Tsin θdθ ...(ii) ⇒ Tcos θ = T_0 cos α = (λgbsin α)cos α = c from (i) d(Tsin θ)=λg(dx)sec θ ⇒ cos θ d(((csin θ)/(cos θ)))=λgdx ⇒ c∫_(tan α) ^( tan θ) ((d(tan θ))/( (√(1+tan^2 θ)))) = λgx let tan θ = z ⇒ ∫_z_0 ^( z) (dz/( (√(1+z^2 )))) = ((λgx)/c) ln (z+(√(1+z^2 )) )∣_z_0 ^z =((λgx)/c) ln (((z+(√(1+z^2 )))/(tan α+sec α)))= ((λgx)/c) ⇒ z+(√(1+z^2 )) =(sec α+tan α) e^(λgx/c) tan θ+sec θ = ke^(μx) ....(A) k = sec α+tan α ; μ= ((λg)/c) Also sec θ−tan θ = (e^(−μx) /k) ...(B) from eq.(A)−eq.(B): we get tan θ = (dy/dx) = (1/2)(ke^(𝛍x) −(e^(−𝛍x) /k)) y = ((k/(2𝛍))e^(𝛍x) +(1/(2𝛍k))e^(−𝛍x) )∣_0 ^x y= (1/(2𝛍))[(ke^(𝛍x) +(1/(ke^(𝛍x) )))−(k+(1/k)) y=(c/(2𝛌g))[k(e^(𝛍x) −1)+(1/k)(e^(−𝛍x) −1)] y= ((bsin αcos α)/2)[k(e^(μx) −1)+(1/k)(e^(−μx) −1)] where k = sec 𝛂+tan 𝛂 and 𝛍= (1/(bsin 𝛂cos 𝛂)) ⇒ y =bsin 𝛂[cosh (((2x)/(bsin 2𝛂)))+sin 𝛂sinh (((2x)/(bsin 2𝛂)))−1].](https://www.tinkutara.com/question/Q45087.png)
$${T}\mathrm{cos}\:\theta{d}\theta+{dT}\mathrm{sin}\:\theta\:=\:\lambda{g}\left({dx}\right)\mathrm{sec}\:\theta\:\:..\left({i}\right) \\ $$$${dT}\mathrm{cos}\:\theta\:=\:{T}\mathrm{sin}\:\theta{d}\theta\:\:\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:{T}\mathrm{cos}\:\theta\:=\:{T}_{\mathrm{0}} \mathrm{cos}\:\alpha\:=\:\left(\lambda{gb}\mathrm{sin}\:\alpha\right)\mathrm{cos}\:\alpha \\ $$$$\:\:\:\:\:\:\:\:=\:\boldsymbol{{c}} \\ $$$${from}\:\left({i}\right) \\ $$$$\:\:\:\:{d}\left({T}\mathrm{sin}\:\theta\right)=\lambda{g}\left({dx}\right)\mathrm{sec}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\theta\:{d}\left(\frac{{c}\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\right)=\lambda{gdx} \\ $$$$\Rightarrow\:{c}\int_{\mathrm{tan}\:\alpha} ^{\:\:\mathrm{tan}\:\theta} \frac{{d}\left(\mathrm{tan}\:\theta\right)}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}}\:=\:\lambda{gx} \\ $$$${let}\:\mathrm{tan}\:\theta\:=\:{z} \\ $$$$\Rightarrow\:\int_{{z}_{\mathrm{0}} } ^{\:\:{z}} \frac{{dz}}{\:\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }}\:=\:\frac{\lambda{gx}}{{c}} \\ $$$$\mathrm{ln}\:\left({z}+\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }\:\right)\mid_{{z}_{\mathrm{0}} } ^{{z}} \:=\frac{\lambda{gx}}{{c}} \\ $$$$\mathrm{ln}\:\left(\frac{{z}+\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }}{\mathrm{tan}\:\alpha+\mathrm{sec}\:\alpha}\right)=\:\frac{\lambda{gx}}{{c}} \\ $$$$\Rightarrow\:{z}+\sqrt{\mathrm{1}+{z}^{\mathrm{2}} }\:=\left(\mathrm{sec}\:\alpha+\mathrm{tan}\:\alpha\right)\:{e}^{\lambda{gx}/{c}} \\ $$$$\:\mathrm{tan}\:\theta+\mathrm{sec}\:\theta\:=\:{ke}^{\mu{x}} \:\:\:\:\:\:\:….\left({A}\right) \\ $$$$\:{k}\:=\:\mathrm{sec}\:\alpha+\mathrm{tan}\:\alpha\:;\:\mu=\:\frac{\lambda{g}}{{c}} \\ $$$${Also}\:\:\mathrm{sec}\:\theta−\mathrm{tan}\:\theta\:=\:\frac{{e}^{−\mu{x}} }{{k}}\:\:\:\:…\left({B}\right) \\ $$$${from}\:{eq}.\left({A}\right)−{eq}.\left({B}\right):\:\:{we}\:{get} \\ $$$$\:\:\mathrm{tan}\:\theta\:=\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left({ke}^{\boldsymbol{\mu{x}}} −\frac{\boldsymbol{{e}}^{−\boldsymbol{\mu{x}}} }{\boldsymbol{{k}}}\right) \\ $$$$\boldsymbol{{y}}\:=\:\left(\frac{\boldsymbol{{k}}}{\mathrm{2}\boldsymbol{\mu}}\boldsymbol{{e}}^{\boldsymbol{\mu{x}}} +\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mu{k}}}\boldsymbol{{e}}^{−\boldsymbol{\mu{x}}} \right)\mid_{\mathrm{0}} ^{\boldsymbol{{x}}} \\ $$$$\boldsymbol{{y}}=\:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mu}}\left[\left(\boldsymbol{{ke}}^{\boldsymbol{\mu{x}}} +\frac{\mathrm{1}}{\boldsymbol{{ke}}^{\boldsymbol{\mu{x}}} }\right)−\left(\boldsymbol{{k}}+\frac{\mathrm{1}}{\boldsymbol{{k}}}\right)\right. \\ $$$$\boldsymbol{{y}}=\frac{\boldsymbol{{c}}}{\mathrm{2}\boldsymbol{\lambda{g}}}\left[\boldsymbol{{k}}\left(\boldsymbol{{e}}^{\boldsymbol{\mu{x}}} −\mathrm{1}\right)+\frac{\mathrm{1}}{\boldsymbol{{k}}}\left(\boldsymbol{{e}}^{−\boldsymbol{\mu{x}}} −\mathrm{1}\right)\right] \\ $$$$\:\:\: \\ $$$${y}=\:\frac{{b}\mathrm{sin}\:\alpha\mathrm{cos}\:\alpha}{\mathrm{2}}\left[{k}\left({e}^{\mu{x}} −\mathrm{1}\right)+\frac{\mathrm{1}}{{k}}\left({e}^{−\mu{x}} −\mathrm{1}\right)\right] \\ $$$${where}\:\boldsymbol{{k}}\:=\:\mathrm{sec}\:\boldsymbol{\alpha}+\mathrm{tan}\:\boldsymbol{\alpha} \\ $$$${and}\:\:\:\:\:\:\boldsymbol{\mu}=\:\frac{\mathrm{1}}{\boldsymbol{{b}}\mathrm{sin}\:\boldsymbol{\alpha}\mathrm{cos}\:\boldsymbol{\alpha}}\: \\ $$$$\Rightarrow\: \\ $$$$\boldsymbol{{y}}\:=\boldsymbol{{b}}\mathrm{sin}\:\boldsymbol{\alpha}\left[\mathrm{cosh}\:\left(\frac{\mathrm{2}\boldsymbol{{x}}}{\boldsymbol{{b}}\mathrm{sin}\:\mathrm{2}\boldsymbol{\alpha}}\right)+\mathrm{sin}\:\boldsymbol{\alpha}\mathrm{sinh}\:\left(\frac{\mathrm{2}\boldsymbol{{x}}}{\boldsymbol{{b}}\mathrm{sin}\:\mathrm{2}\boldsymbol{\alpha}}\right)−\mathrm{1}\right]. \\ $$
Commented by MrW3 last updated on 09/Oct/18
Commented by MrW3 last updated on 09/Oct/18
![in coordinate system uv the rope has the equation v=a cosh (u/a) with a=(T_H /(λg))=b sin α cos α=(1/μ) (dv/du)=sinh (u/a) at (u_1 ,v_1 ): sinh (u_1 /a)=tan α ⇒(u_1 /a)=sinh^(−1) (tan α)=ln (tan α+(√(1+tan^2 α))) =ln (tan α+sec α)=ln k v_1 =a cosh (u_1 /a)=a cosh (ln k)=a×((k+(1/k))/2) =(1/(2μ))(k+(1/k)) u=u_1 +x v=v_1 +y v_1 +y=a cosh ((u_1 +x)/a) (1/(2μ))(k+(1/k))+y=(1/μ) cosh (ln k+μx) (1/(2μ))(k+(1/k))+y=(1/(2μ)) (e^(ln k+μx) +e^(−ln k−μx) ) (1/(2μ))(k+(1/k))+y=(1/(2μ)) (ke^(μx) +(1/k)e^(−μx) ) ⇒y=(1/(2μ)) [k(e^(μx) −1)+(1/k)(e^(−μx) −1)]](https://www.tinkutara.com/question/Q45108.png)
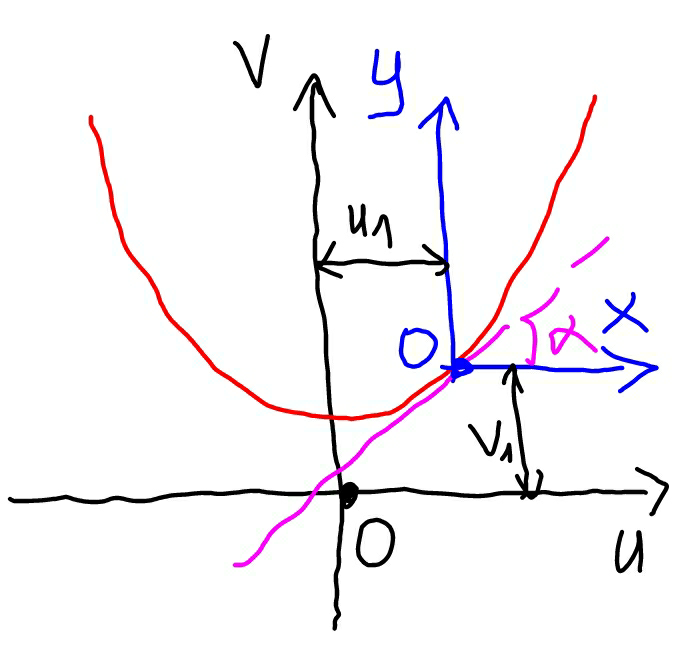
$${in}\:{coordinate}\:{system}\:{uv}\:{the}\:{rope} \\ $$$${has}\:{the}\:{equation} \\ $$$${v}={a}\:\mathrm{cosh}\:\frac{{u}}{{a}} \\ $$$${with}\:{a}=\frac{{T}_{{H}} }{\lambda{g}}={b}\:\mathrm{sin}\:\alpha\:\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\mu} \\ $$$$\frac{{dv}}{{du}}=\mathrm{sinh}\:\frac{{u}}{{a}} \\ $$$${at}\:\left({u}_{\mathrm{1}} ,{v}_{\mathrm{1}} \right): \\ $$$$\mathrm{sinh}\:\frac{{u}_{\mathrm{1}} }{{a}}=\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\frac{{u}_{\mathrm{1}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\alpha\right)=\mathrm{ln}\:\left(\mathrm{tan}\:\alpha+\sqrt{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\alpha}\right) \\ $$$$=\mathrm{ln}\:\left(\mathrm{tan}\:\alpha+\mathrm{sec}\:\alpha\right)=\mathrm{ln}\:{k} \\ $$$${v}_{\mathrm{1}} ={a}\:\mathrm{cosh}\:\frac{{u}_{\mathrm{1}} }{{a}}={a}\:\mathrm{cosh}\:\left(\mathrm{ln}\:{k}\right)={a}×\frac{{k}+\frac{\mathrm{1}}{{k}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\mu}\left({k}+\frac{\mathrm{1}}{{k}}\right) \\ $$$$ \\ $$$${u}={u}_{\mathrm{1}} +{x} \\ $$$${v}={v}_{\mathrm{1}} +{y} \\ $$$${v}_{\mathrm{1}} +{y}={a}\:\mathrm{cosh}\:\frac{{u}_{\mathrm{1}} +{x}}{{a}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\mu}\left({k}+\frac{\mathrm{1}}{{k}}\right)+{y}=\frac{\mathrm{1}}{\mu}\:\mathrm{cosh}\:\left(\mathrm{ln}\:{k}+\mu{x}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\mu}\left({k}+\frac{\mathrm{1}}{{k}}\right)+{y}=\frac{\mathrm{1}}{\mathrm{2}\mu}\:\left({e}^{\mathrm{ln}\:{k}+\mu{x}} +{e}^{−\mathrm{ln}\:{k}−\mu{x}} \right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}\mu}\left({k}+\frac{\mathrm{1}}{{k}}\right)+{y}=\frac{\mathrm{1}}{\mathrm{2}\mu}\:\left({ke}^{\mu{x}} +\frac{\mathrm{1}}{{k}}{e}^{−\mu{x}} \right) \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{2}\mu}\:\left[{k}\left({e}^{\mu{x}} −\mathrm{1}\right)+\frac{\mathrm{1}}{{k}}\left({e}^{−\mu{x}} −\mathrm{1}\right)\right] \\ $$
Commented by ajfour last updated on 08/Oct/18
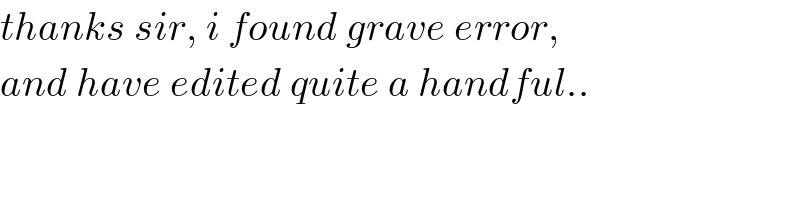
$${thanks}\:{sir},\:{i}\:{found}\:{grave}\:{error}, \\ $$$${and}\:{have}\:{edited}\:{quite}\:{a}\:{handful}.. \\ $$
Commented by ajfour last updated on 08/Oct/18
$${genuine}\:{point},\:{Sir}. \\ $$
Commented by MrW3 last updated on 09/Oct/18

$${sir}\:{you}\:{have}\:{solved}\:{the}\:{problem}\:{from} \\ $$$${the}\:{root},\:{it}'{s}\:{perfect}!\:{wonderful}! \\ $$
Commented by ajfour last updated on 09/Oct/18
$${thank}\:{you}\:{so}\:{much}\:{Sir}!\:{shall}\:{no} \\ $$$${more}\:{be}\:{all}-{afraid}\:{of}\:{hyperbolic}\:{functions}. \\ $$
Commented by MrW3 last updated on 09/Oct/18

$${it}'{s}\:{a}\:{great}\:{and}\:{ingenious}\:{trick}\:{to}\:{get} \\ $$$$\boldsymbol{\theta}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{2}}−\mathrm{2tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{ke}^{\mu{x}} }\:{from} \\ $$$$\:\frac{\mathrm{1}+\mathrm{sin}\:\theta}{\mathrm{cos}\:\theta}\:=\:{ke}^{\boldsymbol{\mu{x}}} \\ $$$${I}\:{shall}\:{keep}\:{this}\:{in}\:{mind}. \\ $$
