Question Number 49898 by Raj Singh last updated on 12/Dec/18
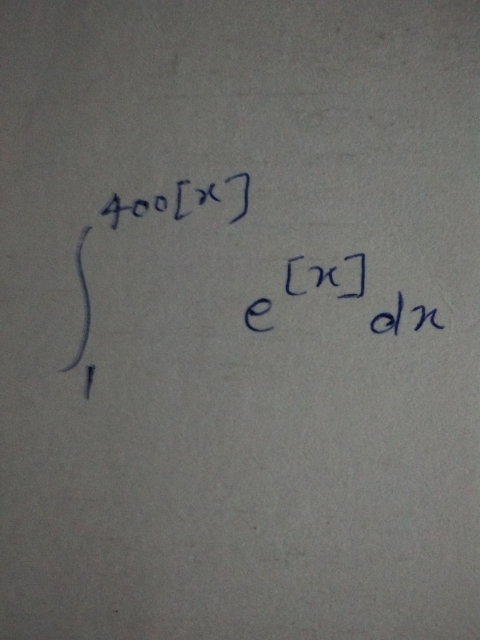
Commented by Abdo msup. last updated on 12/Dec/18
![I =∫_1 ^(400[x]) e^([t]) dt =Σ_(k=1) ^(400[x]−1) ∫_k ^(k+1) e^k dt =Σ_(k=1) ^(400[x]−1) e^k = ((1−e^(400[x]) )/(1−e)) −1 =((1−e^(400[x]) −1+e)/(1−e)) =((e−e^(400[x]) )/(1−e)) =](https://www.tinkutara.com/question/Q49931.png)
$${I}\:=\int_{\mathrm{1}} ^{\mathrm{400}\left[{x}\right]} \:\:{e}^{\left[{t}\right]} {dt}\:=\sum_{{k}=\mathrm{1}} ^{\mathrm{400}\left[{x}\right]−\mathrm{1}} \:\int_{{k}} ^{{k}+\mathrm{1}} \:{e}^{{k}} \:{dt} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{\mathrm{400}\left[{x}\right]−\mathrm{1}} \:{e}^{{k}} \:=\:\frac{\mathrm{1}−{e}^{\mathrm{400}\left[{x}\right]} }{\mathrm{1}−{e}}\:−\mathrm{1}\:=\frac{\mathrm{1}−{e}^{\mathrm{400}\left[{x}\right]} −\mathrm{1}+{e}}{\mathrm{1}−{e}} \\ $$$$=\frac{{e}−{e}^{\mathrm{400}\left[{x}\right]} }{\mathrm{1}−{e}} \\ $$$$= \\ $$
