Question Number 51181 by ajfour last updated on 24/Dec/18
Commented by ajfour last updated on 24/Dec/18
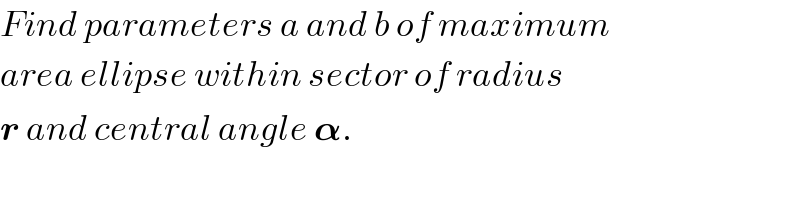
$${Find}\:{parameters}\:{a}\:{and}\:{b}\:{of}\:{maximum} \\ $$$${area}\:{ellipse}\:{within}\:{sector}\:{of}\:{radius} \\ $$$$\boldsymbol{{r}}\:{and}\:{central}\:{angle}\:\boldsymbol{\alpha}. \\ $$
Answered by mr W last updated on 24/Dec/18
Commented by mr W last updated on 25/Dec/18
![eqn. of ellipse: (x^2 /a^2 )+(((yβc)^2 )/b^2 )=1 eqn. of OQ: y=x tan ((Ο/2)β(Ξ±/2))=(x/(tan (Ξ±/2)))=mx βa^2 m^2 +b^2 =c^2 eqn. of circle: x^2 +y^2 =r^2 ((r^2 βy^2 )/a^2 )+(((yβc)^2 )/b^2 )=1 case 1: Ξ±β€90Β° (((rβc)^2 )/b^2 )=1 βb^2 =(rβc)^2 βa^2 m^2 =c^2 β(rβc)^2 =r(2cβr) P=a^2 b^2 m^2 =r(2cβr)(rβc)^2 (dP/dc)=0 2(rβc)^2 β(2cβr)2(rβc)=0 βc=((2r)/3) βb^2 =(r^2 /9) βa^2 =((c^2 βb^2 )/m^2 )=(r^2 /(3m^2 )) case 2: 90Β°β€Ξ±β€180Β° b^2 r^2 βb^2 y^2 +a^2 (y^2 β2cy+c^2 )=a^2 b^2 (a^2 βb^2 )y^2 β2a^2 cy+a^2 c^2 +b^2 (r^2 βa^2 )=0 D=4a^4 c^2 β4(a^2 βb^2 )(a^2 c^2 +b^2 r^2 βa^2 b^2 )=0 β(a^2 βb^2 )(r^2 βa^2 )=a^2 c^2 β(a^2 βb^2 )(r^2 βa^2 )=a^2 (a^2 m^2 +b^2 ) let P=a^2 b^2 β(a^2 β(P/a^2 ))(r^2 βa^2 )=a^2 (a^2 m^2 +(P/a^2 )) β(a^4 βP)(r^2 βa^2 )=a^2 (a^4 m^2 +P) (dP/da)=0 (a^4 βP)(β2a)+(4a^3 )(r^2 βa^2 )=2a(a^4 m^2 +P)+a^2 (4a^3 m^2 ) 3a^2 (m^2 +1)=2r^2 βa^2 =((2r^2 )/(3(m^2 +1)))βa=r(β(2/3)) sin (Ξ±/2) β(a^2 βb^2 )(r^2 βa^2 )=a^2 (a^2 m^2 +b^2 ) βb^2 r^2 =a^2 [r^2 βa^2 (m^2 +1)] βb^2 =(a^2 /3)=((2r^2 )/(9(m^2 +1)))βb=r((β2)/3) sin (Ξ±/2) βc^2 =a^2 m^2 +b^2 =((2(3m^2 +1)r^2 )/(9(m^2 +1)))βc=((r(β(2(2+cos Ξ±))))/3) condition: c+bβ€r ((r(β(2(2+cos Ξ±))))/3)+r((β2)/3) sin (Ξ±/2)β€r βsin (Ξ±/2)β₯(1/( (β2))) β(Ξ±/2)β₯(Ο/4) βΞ±β₯(Ο/2)](https://www.tinkutara.com/question/Q51203.png)
$${eqn}.\:{of}\:{ellipse}: \\ $$$$\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}β{c}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${eqn}.\:{of}\:{OQ}: \\ $$$${y}={x}\:\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}β\frac{\alpha}{\mathrm{2}}\right)=\frac{{x}}{\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}}={mx} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{circle}: \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\frac{{r}^{\mathrm{2}} β{y}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}β{c}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:\alpha\leqslant\mathrm{90}Β° \\ $$$$\frac{\left({r}β{c}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$$\Rightarrow{b}^{\mathrm{2}} =\left({r}β{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {m}^{\mathrm{2}} ={c}^{\mathrm{2}} β\left({r}β{c}\right)^{\mathrm{2}} ={r}\left(\mathrm{2}{c}β{r}\right) \\ $$$${P}={a}^{\mathrm{2}} {b}^{\mathrm{2}} {m}^{\mathrm{2}} ={r}\left(\mathrm{2}{c}β{r}\right)\left({r}β{c}\right)^{\mathrm{2}} \\ $$$$\frac{{dP}}{{dc}}=\mathrm{0} \\ $$$$\mathrm{2}\left({r}β{c}\right)^{\mathrm{2}} β\left(\mathrm{2}{c}β{r}\right)\mathrm{2}\left({r}β{c}\right)=\mathrm{0} \\ $$$$\Rightarrow{c}=\frac{\mathrm{2}{r}}{\mathrm{3}} \\ $$$$\Rightarrow{b}^{\mathrm{2}} =\frac{{r}^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{{c}^{\mathrm{2}} β{b}^{\mathrm{2}} }{{m}^{\mathrm{2}} }=\frac{{r}^{\mathrm{2}} }{\mathrm{3}{m}^{\mathrm{2}} } \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:\mathrm{90}Β°\leqslant\alpha\leqslant\mathrm{180}Β° \\ $$$${b}^{\mathrm{2}} {r}^{\mathrm{2}} β{b}^{\mathrm{2}} {y}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({y}^{\mathrm{2}} β\mathrm{2}{cy}+{c}^{\mathrm{2}} \right)={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\left({a}^{\mathrm{2}} β{b}^{\mathrm{2}} \right){y}^{\mathrm{2}} β\mathrm{2}{a}^{\mathrm{2}} {cy}+{a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} \left({r}^{\mathrm{2}} β{a}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${D}=\mathrm{4}{a}^{\mathrm{4}} {c}^{\mathrm{2}} β\mathrm{4}\left({a}^{\mathrm{2}} β{b}^{\mathrm{2}} \right)\left({a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {r}^{\mathrm{2}} β{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} β{b}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} β{a}^{\mathrm{2}} \right)={a}^{\mathrm{2}} {c}^{\mathrm{2}} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} β{b}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} β{a}^{\mathrm{2}} \right)={a}^{\mathrm{2}} \left({a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$${let}\:{P}={a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} β\frac{{P}}{{a}^{\mathrm{2}} }\right)\left({r}^{\mathrm{2}} β{a}^{\mathrm{2}} \right)={a}^{\mathrm{2}} \left({a}^{\mathrm{2}} {m}^{\mathrm{2}} +\frac{{P}}{{a}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow\left({a}^{\mathrm{4}} β{P}\right)\left({r}^{\mathrm{2}} β{a}^{\mathrm{2}} \right)={a}^{\mathrm{2}} \left({a}^{\mathrm{4}} {m}^{\mathrm{2}} +{P}\right) \\ $$$$\frac{{dP}}{{da}}=\mathrm{0} \\ $$$$\left({a}^{\mathrm{4}} β{P}\right)\left(β\mathrm{2}{a}\right)+\left(\mathrm{4}{a}^{\mathrm{3}} \right)\left({r}^{\mathrm{2}} β{a}^{\mathrm{2}} \right)=\mathrm{2}{a}\left({a}^{\mathrm{4}} {m}^{\mathrm{2}} +{P}\right)+{a}^{\mathrm{2}} \left(\mathrm{4}{a}^{\mathrm{3}} {m}^{\mathrm{2}} \right) \\ $$$$\mathrm{3}{a}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{1}\right)=\mathrm{2}{r}^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} =\frac{\mathrm{2}{r}^{\mathrm{2}} }{\mathrm{3}\left({m}^{\mathrm{2}} +\mathrm{1}\right)}\Rightarrow{a}={r}\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow\left({a}^{\mathrm{2}} β{b}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} β{a}^{\mathrm{2}} \right)={a}^{\mathrm{2}} \left({a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{b}^{\mathrm{2}} {r}^{\mathrm{2}} ={a}^{\mathrm{2}} \left[{r}^{\mathrm{2}} β{a}^{\mathrm{2}} \left({m}^{\mathrm{2}} +\mathrm{1}\right)\right] \\ $$$$\Rightarrow{b}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{3}}=\frac{\mathrm{2}{r}^{\mathrm{2}} }{\mathrm{9}\left({m}^{\mathrm{2}} +\mathrm{1}\right)}\Rightarrow{b}={r}\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$$$\Rightarrow{c}^{\mathrm{2}} ={a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} =\frac{\mathrm{2}\left(\mathrm{3}{m}^{\mathrm{2}} +\mathrm{1}\right){r}^{\mathrm{2}} }{\mathrm{9}\left({m}^{\mathrm{2}} +\mathrm{1}\right)}\Rightarrow{c}=\frac{{r}\sqrt{\mathrm{2}\left(\mathrm{2}+\mathrm{cos}\:\alpha\right)}}{\mathrm{3}} \\ $$$${condition}:\:{c}+{b}\leqslant{r} \\ $$$$\frac{{r}\sqrt{\mathrm{2}\left(\mathrm{2}+\mathrm{cos}\:\alpha\right)}}{\mathrm{3}}+{r}\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\:\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\leqslant{r} \\ $$$$\Rightarrow\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\geqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\Rightarrow\frac{\alpha}{\mathrm{2}}\geqslant\frac{\pi}{\mathrm{4}}\:\Rightarrow\alpha\geqslant\frac{\pi}{\mathrm{2}} \\ $$
Commented by mr W last updated on 24/Dec/18
Commented by mr W last updated on 24/Dec/18
Commented by mr W last updated on 24/Dec/18
Commented by ajfour last updated on 25/Dec/18
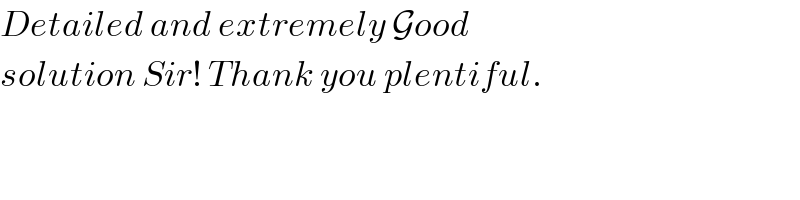
$${Detailed}\:{and}\:{extremely}\:\mathcal{G}{ood} \\ $$$${solution}\:{Sir}!\:{Thank}\:{you}\:{plentiful}. \\ $$
Answered by MJS last updated on 24/Dec/18
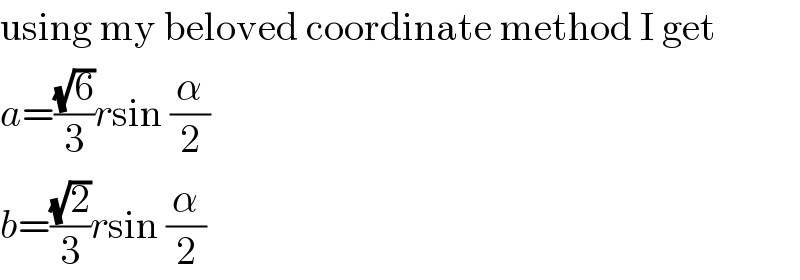
$$\mathrm{using}\:\mathrm{my}\:\mathrm{beloved}\:\mathrm{coordinate}\:\mathrm{method}\:\mathrm{I}\:\mathrm{get} \\ $$$${a}=\frac{\sqrt{\mathrm{6}}}{\mathrm{3}}{r}\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$$${b}=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}{r}\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$
Commented by MJS last updated on 24/Dec/18
$$\mathrm{you}'\mathrm{re}\:\mathrm{right}.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{checking}! \\ $$
Commented by mr W last updated on 24/Dec/18
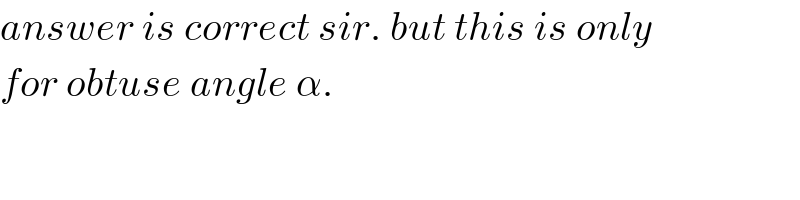
$${answer}\:{is}\:{correct}\:{sir}.\:{but}\:{this}\:{is}\:{only} \\ $$$${for}\:{obtuse}\:{angle}\:\alpha. \\ $$