Question Number 52161 by naka3546 last updated on 03/Jan/19

Commented by prakash jain last updated on 04/Jan/19
![f(x)= { ((7x+1),(0≤x≤1/2)),((7−5x),(1/2≤x≤1)) :} ∫_0 ^1 f(x)dx=∫_0 ^(1/2) f(x)dx+∫_(1 /2) ^1 f(x)dx =[((7x^2 )/2)+x]_0 ^(1/2) +[7x−((5x^2 )/2)]_(1/2) ^1 =((7/8)+(1/2))+(7−(5/2))−((7/2)−(5/8)) =((7+4+56−20−28+5)/8)=((24)/3)=3 f(x) above satifies all conditons. f(0)=1 f(1)=2 ∫_0 ^1 f(x)dx=3 xf(x)>0 for 0<x<1 ∫_0 ^1 xf(x)dx is unlikely to be 0. You can re−check. I will my workinhs again.](https://www.tinkutara.com/question/Q52176.png)
$${f}\left({x}\right)=\begin{cases}{\mathrm{7}{x}+\mathrm{1}}&{\mathrm{0}\leqslant{x}\leqslant\mathrm{1}/\mathrm{2}}\\{\mathrm{7}−\mathrm{5}{x}}&{\mathrm{1}/\mathrm{2}\leqslant{x}\leqslant\mathrm{1}}\end{cases} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} {f}\left({x}\right){dx}+\int_{\mathrm{1}\:/\mathrm{2}} ^{\mathrm{1}} {f}\left({x}\right){dx} \\ $$$$=\left[\frac{\mathrm{7}{x}^{\mathrm{2}} }{\mathrm{2}}+{x}\right]_{\mathrm{0}} ^{\mathrm{1}/\mathrm{2}} +\left[\mathrm{7}{x}−\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{1}/\mathrm{2}} ^{\mathrm{1}} \\ $$$$=\left(\frac{\mathrm{7}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\mathrm{7}−\frac{\mathrm{5}}{\mathrm{2}}\right)−\left(\frac{\mathrm{7}}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{8}}\right) \\ $$$$=\frac{\mathrm{7}+\mathrm{4}+\mathrm{56}−\mathrm{20}−\mathrm{28}+\mathrm{5}}{\mathrm{8}}=\frac{\mathrm{24}}{\mathrm{3}}=\mathrm{3} \\ $$$${f}\left({x}\right)\:{above}\:{satifies}\:{all}\:{conditons}. \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\mathrm{3} \\ $$$${xf}\left({x}\right)>\mathrm{0}\:{for}\:\mathrm{0}<{x}<\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {xf}\left({x}\right){dx}\:\mathrm{is}\:\mathrm{unlikely}\:\mathrm{to}\:\mathrm{be}\:\mathrm{0}. \\ $$$$ \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{re}−\mathrm{check}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{my}\:\mathrm{workinhs} \\ $$$$\mathrm{again}. \\ $$
Commented by mr W last updated on 04/Jan/19

$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\:{represents}\:{the}\:{area}.\:{the} \\ $$$${area}\:{is}\:\mathrm{3}.\:{but}\:{infinitely}\:{many}\:{shapes} \\ $$$${can}\:{have}\:{the}\:{same}\:{area}. \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {xf}\left({x}\right){dx}\:{represents}\:{the}\:{statical}\:{moment} \\ $$$${of}\:{the}\:{area}\:{about}\:{y}−{axis}.\:{it}\:{depends} \\ $$$${not}\:{only}\:{on}\:{the}\:{size}\:{of}\:{the}\:{area}\:{but} \\ $$$${also}\:{on}\:{how}\:{the}\:{area}\:{is}\:{distributed}, \\ $$$${i}.{e}.\:{on}\:{the}\:{shape}\:{of}\:{the}\:{area},\:{or}\:{the} \\ $$$${position}\:{of}\:{area}'{s}\:{centeroid}. \\ $$$${when}\:{only}\:{the}\:{area}\:{is}\:{given},\:{the}\:{statical} \\ $$$${moment}\:{is}\:{not}\:{unique}. \\ $$$${for}\:{example}:\:{the}\:{dotted}\:{shape}\:{has}\:{the} \\ $$$${same}\:{area}\:{as}\:{the}\:{solid}\:{shape},\:{but}\:{they} \\ $$$${have}\:{different}\:{statical}\:{moment}\:{about} \\ $$$${y}−{axis},\:{because}\:{they}\:{have}\:{different} \\ $$$${position}\:{of}\:{centroid}. \\ $$$${this}\:{is}\:{the}\:{reason}\:{why}\:\int_{\mathrm{0}} ^{\mathrm{1}} {xf}\left({x}\right){dx}\:{can} \\ $$$${not}\:{be}\:{unique}\:{determined}\:{with}\:{the} \\ $$$${given}\:{conditions}. \\ $$
Commented by mr W last updated on 04/Jan/19

Commented by mr W last updated on 04/Jan/19

$${there}\:{is}\:{no}\:{unique}\:{solution}. \\ $$
Commented by Otchere Abdullai last updated on 04/Jan/19

$${please}\:{which}\:{app}\:{did}\:{you}\:{use}\:{for}\:{your} \\ $$$${sketch}?\:\:{i}\:{want}\:{to}\:{download} \\ $$
Commented by mr W last updated on 04/Jan/19
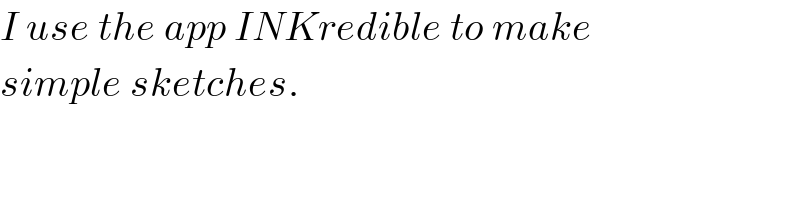
$${I}\:{use}\:{the}\:{app}\:{INKredible}\:{to}\:{make} \\ $$$${simple}\:{sketches}. \\ $$
Commented by Otchere Abdullai last updated on 04/Jan/19

$${thank}\:{you}\:{sir} \\ $$
Answered by pooja24 last updated on 04/Jan/19
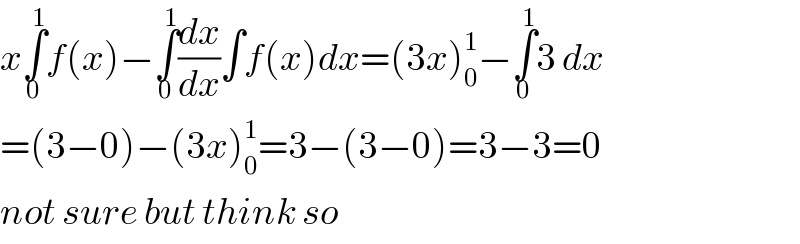
$${x}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right)−\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{{dx}}\int{f}\left({x}\right){dx}=\left(\mathrm{3}{x}\right)_{\mathrm{0}} ^{\mathrm{1}} −\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{3}\:{dx} \\ $$$$=\left(\mathrm{3}−\mathrm{0}\right)−\left(\mathrm{3}{x}\right)_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{3}−\left(\mathrm{3}−\mathrm{0}\right)=\mathrm{3}−\mathrm{3}=\mathrm{0} \\ $$$${not}\:{sure}\:{but}\:{think}\:{so} \\ $$
Commented by prakash jain last updated on 04/Jan/19
![x∫_0 ^1 f(x)−∫_0 ^1 (dx/dx)∫f(x)dx=(3x)_0 ^1 −∫_0 ^1 3 dx You can not write ∫_0 ^1 [∫f(x)dx]dx as ∫_0 ^1 [∫_0 ^1 f(x)dx]dx You have evaluated internal integral first.](https://www.tinkutara.com/question/Q52177.png)
$${x}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right)−\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{{dx}}\int{f}\left({x}\right){dx}=\left(\mathrm{3}{x}\right)_{\mathrm{0}} ^{\mathrm{1}} −\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{3}\:{dx} \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{not}\:\mathrm{write} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left[\int{f}\left({x}\right){dx}\right]{dx}\:{as}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left[\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}\right]{dx} \\ $$$$\mathrm{You}\:\mathrm{have}\:\mathrm{evaluated}\:\mathrm{internal}\:\mathrm{integral} \\ $$$$\mathrm{first}. \\ $$
Answered by MJS last updated on 04/Jan/19
![if it′s a polynome f(x)=ax^2 +bx+c F(x)=(a/3)x^3 +(b/2)x^2 +cx (1) c=1 (2) a+b+1=2 ⇒ a+b=1 (3) (a/3)+(b/2)+1=3 ⇒ 2a+3b=12 ⇒ b=10, a=−9 f(x)=−9x^2 +10x+1 ∫_0 ^1 xf(x)dx=∫_0 ^1 (−9x^3 +10x^2 +x)dx= =[−(9/4)x^4 +((10)/3)x^3 +(1/2)x^2 ]_0 ^1 =((19)/(12))](https://www.tinkutara.com/question/Q52180.png)
$$\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{polynome} \\ $$$${f}\left({x}\right)={ax}^{\mathrm{2}} +{bx}+{c} \\ $$$${F}\left({x}\right)=\frac{{a}}{\mathrm{3}}{x}^{\mathrm{3}} +\frac{{b}}{\mathrm{2}}{x}^{\mathrm{2}} +{cx} \\ $$$$\left(\mathrm{1}\right)\:\:\:{c}=\mathrm{1} \\ $$$$\left(\mathrm{2}\right)\:\:\:{a}+{b}+\mathrm{1}=\mathrm{2}\:\Rightarrow\:{a}+{b}=\mathrm{1} \\ $$$$\left(\mathrm{3}\right)\:\:\:\frac{{a}}{\mathrm{3}}+\frac{{b}}{\mathrm{2}}+\mathrm{1}=\mathrm{3}\:\Rightarrow\:\mathrm{2}{a}+\mathrm{3}{b}=\mathrm{12} \\ $$$$\Rightarrow\:{b}=\mathrm{10},\:{a}=−\mathrm{9} \\ $$$${f}\left({x}\right)=−\mathrm{9}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{1} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{xf}\left({x}\right){dx}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(−\mathrm{9}{x}^{\mathrm{3}} +\mathrm{10}{x}^{\mathrm{2}} +{x}\right){dx}= \\ $$$$=\left[−\frac{\mathrm{9}}{\mathrm{4}}{x}^{\mathrm{4}} +\frac{\mathrm{10}}{\mathrm{3}}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{19}}{\mathrm{12}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 04/Jan/19
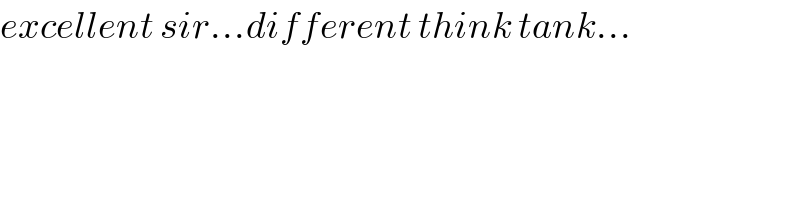
$${excellent}\:{sir}…{different}\:{think}\:{tank}… \\ $$
