Question Number 53881 by ajfour last updated on 26/Jan/19

Commented by ajfour last updated on 26/Jan/19
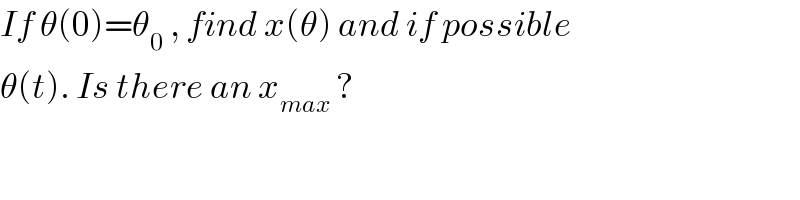
$${If}\:\theta\left(\mathrm{0}\right)=\theta_{\mathrm{0}} \:,\:{find}\:{x}\left(\theta\right)\:{and}\:{if}\:{possible} \\ $$$$\theta\left({t}\right).\:{Is}\:{there}\:{an}\:{x}_{{max}} \:? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Jan/19
![when time is t position of rod as shown[as dotted 1) here Torque is variable as m mass move 2)Torque at time t is Mg(L/2)cosθ(t)+mg(L−x(θ)cosθ(t)=(d/dt)(Iw) Right hand side=w(d/dt)[((ML^2 )/3)+m{(L−x(θ)}^2 ]+[((ML^2 )/3)+m{(L−x(θ)}^2 ]α =w{2m(L−x)(dx/dt)}+[M(L^2 /3)+m(L−x)^2 ](dw/dt) continue...](https://www.tinkutara.com/question/Q54010.png)
$${when}\:{time}\:{is}\:{t}\:{position}\:{of}\:{rod}\:{as}\:{shown}\left[{as}\:{dotted}\right. \\ $$$$\left.\mathrm{1}\right)\:{here}\:{Torque}\:{is}\:{variable}\:{as}\:{m}\:{mass}\:{move} \\ $$$$\left.\mathrm{2}\right){Torque}\:{at}\:{time}\:{t}\:{is} \\ $$$$\:\:{Mg}\frac{{L}}{\mathrm{2}}{cos}\theta\left({t}\right)+{mg}\left({L}−{x}\left(\theta\right){cos}\theta\left({t}\right)=\frac{{d}}{{dt}}\left({Iw}\right)\right. \\ $$$${Right}\:{hand}\:{side}={w}\frac{{d}}{{dt}}\left[\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}+{m}\left\{\left({L}−{x}\left(\theta\right)\right\}^{\mathrm{2}} \right]+\left[\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}+{m}\left\{\left({L}−{x}\left(\theta\right)\right\}^{\mathrm{2}} \right]\alpha\right.\right. \\ $$$$={w}\left\{\mathrm{2}{m}\left({L}−{x}\right)\frac{{dx}}{{dt}}\right\}+\left[{M}\frac{{L}^{\mathrm{2}} }{\mathrm{3}}+{m}\left({L}−{x}\right)^{\mathrm{2}} \right]\frac{{dw}}{{dt}} \\ $$$${continue}… \\ $$
