Question Number 55100 by aseerimad last updated on 17/Feb/19
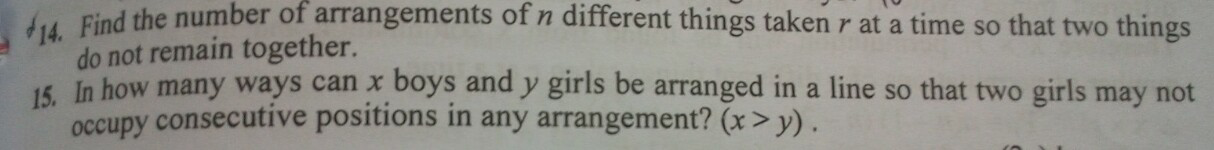
Commented by aseerimad last updated on 17/Feb/19
how no.14 is done?.....pls help
Commented by aseerimad last updated on 17/Feb/19
thank you sir. But can u please convert the answer to the form that I gave?
Commented by aseerimad last updated on 17/Feb/19
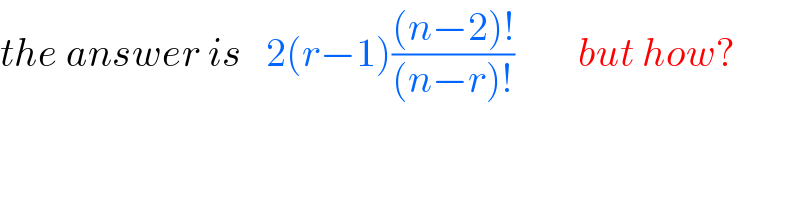
$${the}\:{answer}\:{is}\:\:\:\mathrm{2}\left({r}−\mathrm{1}\right)\frac{\left({n}−\mathrm{2}\right)!}{\left({n}−{r}\right)!}\:\:\:\:\:\:\:\:{but}\:{how}? \\ $$
Commented by mr W last updated on 17/Feb/19
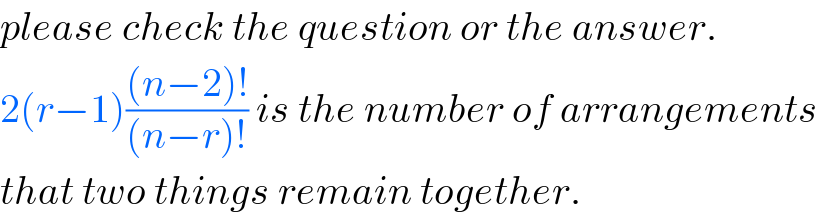
$${please}\:{check}\:{the}\:{question}\:{or}\:{the}\:{answer}. \\ $$$$\mathrm{2}\left({r}−\mathrm{1}\right)\frac{\left({n}−\mathrm{2}\right)!}{\left({n}−{r}\right)!}\:{is}\:{the}\:{number}\:{of}\:{arrangements} \\ $$$${that}\:{two}\:{things}\:{remain}\:{together}. \\ $$
Commented by aseerimad last updated on 17/Feb/19
sorry. actually these are what I got. May be there's a problem with the answer. Thanks anyway for your efforts!
Answered by mr W last updated on 17/Feb/19
![we take r things from n things with r≥2. there are totally P_r ^( n) ways. number of ways such that two things (say A and B) are together: we take the rest r−2 things from the rest n−2 things, there are C_(r−2) ^( n−2) ways to do that. since A and B should be together, as AB or as BA, we arrange in fact r−1 things, i.e. AB and the rest r−2 things, there are 2×(r−1)! arrangements, totally there are C_(r−2) ^( n−2) ×2×(r−1)! ways that the two things are together. therefore number of ways such that two things are not together is P_r ^( n) −C_(r−2) ^(n−2) ×2×(r−1)! =((n!)/((n−r)!))−(((n−2)!×2×(r−1)!)/((r−2)!(n−r)!)) =((n(n−1)(n−2)!)/((n−r)!))−(((n−2)!×2×(r−1))/((n−r)!)) =(((n−2)!)/((n−r)!))[n(n−1)−2(r−1)]](https://www.tinkutara.com/question/Q55112.png)
$${we}\:{take}\:{r}\:{things}\:{from}\:{n}\:{things}\:{with}\:{r}\geqslant\mathrm{2}. \\ $$$${there}\:{are}\:{totally}\:{P}_{{r}} ^{\:{n}} \:{ways}. \\ $$$${number}\:{of}\:{ways}\:{such}\:{that}\:{two}\:{things} \\ $$$$\left({say}\:{A}\:{and}\:{B}\right)\:{are}\:{together}: \\ $$$${we}\:{take}\:{the}\:{rest}\:{r}−\mathrm{2}\:{things}\:{from}\:{the} \\ $$$${rest}\:{n}−\mathrm{2}\:{things},\:{there}\:{are}\:{C}_{{r}−\mathrm{2}} ^{\:{n}−\mathrm{2}} \:{ways}\:{to} \\ $$$${do}\:{that}.\:{since}\:{A}\:{and}\:{B}\:{should}\:{be}\:{together}, \\ $$$${as}\:{AB}\:{or}\:{as}\:{BA},\:{we}\:{arrange}\:{in}\:{fact} \\ $$$${r}−\mathrm{1}\:{things},\:{i}.{e}.\:{AB}\:{and}\:{the}\:{rest}\:{r}−\mathrm{2} \\ $$$${things},\:{there}\:{are}\:\mathrm{2}×\left({r}−\mathrm{1}\right)!\:{arrangements}, \\ $$$${totally}\:{there}\:{are}\:{C}_{{r}−\mathrm{2}} ^{\:{n}−\mathrm{2}} ×\mathrm{2}×\left({r}−\mathrm{1}\right)!\:{ways} \\ $$$${that}\:{the}\:{two}\:{things}\:{are}\:{together}. \\ $$$${therefore}\:{number}\:{of}\:{ways}\:{such}\:{that} \\ $$$${two}\:{things}\:{are}\:{not}\:{together}\:{is} \\ $$$${P}_{{r}} ^{\:{n}} −{C}_{{r}−\mathrm{2}} ^{{n}−\mathrm{2}} ×\mathrm{2}×\left({r}−\mathrm{1}\right)! \\ $$$$=\frac{{n}!}{\left({n}−{r}\right)!}−\frac{\left({n}−\mathrm{2}\right)!×\mathrm{2}×\left({r}−\mathrm{1}\right)!}{\left({r}−\mathrm{2}\right)!\left({n}−{r}\right)!} \\ $$$$=\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)!}{\left({n}−{r}\right)!}−\frac{\left({n}−\mathrm{2}\right)!×\mathrm{2}×\left({r}−\mathrm{1}\right)}{\left({n}−{r}\right)!} \\ $$$$=\frac{\left({n}−\mathrm{2}\right)!}{\left({n}−{r}\right)!}\left[{n}\left({n}−\mathrm{1}\right)−\mathrm{2}\left({r}−\mathrm{1}\right)\right] \\ $$
Commented by aseerimad last updated on 17/Feb/19
may the Almighty bless you with goodness!
