Question Number 55211 by naka3546 last updated on 19/Feb/19

Answered by tanmay.chaudhury50@gmail.com last updated on 19/Feb/19
![approach.. ((a^2 +(b−1)^2 )/2)≥(√(a^2 ×(b−1)^2 )) x^2 ≥2a(b−1) y^2 ≥2b(c−1) z^2 ≥2c(a−1) since x^2 =+ve so b>1 and a>0 for min value of x [ b=1] similarly for min value of y [c=1] for min value of z [a=1] x+y+z =(√(a^2 +(b−1)^2 )) +(√(b^2 +(c−1)^2 )) +(√(c^2 +(a−1)^2 )) =(√(1+0)) +(√(1+0)) +(√(1+0)) =3(min value)...](https://www.tinkutara.com/question/Q55221.png)
$$ \\ $$$$ \\ $$$$ \\ $$$${approach}.. \\ $$$$\frac{{a}^{\mathrm{2}} +\left({b}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}\geqslant\sqrt{{a}^{\mathrm{2}} ×\left({b}−\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$${x}^{\mathrm{2}} \geqslant\mathrm{2}{a}\left({b}−\mathrm{1}\right) \\ $$$${y}^{\mathrm{2}} \geqslant\mathrm{2}{b}\left({c}−\mathrm{1}\right) \\ $$$${z}^{\mathrm{2}} \geqslant\mathrm{2}{c}\left({a}−\mathrm{1}\right) \\ $$$${since}\:{x}^{\mathrm{2}} =+{ve}\:{so}\:{b}>\mathrm{1}\:{and}\:{a}>\mathrm{0} \\ $$$${for}\:{min}\:{value}\:{of}\:{x}\:\:\:\left[\:{b}=\mathrm{1}\right] \\ $$$${similarly}\:{for}\:{min}\:{value}\:{of}\:{y}\:\:\:\:\left[{c}=\mathrm{1}\right] \\ $$$${for}\:{min}\:{value}\:{of}\:{z}\:\:\:\left[{a}=\mathrm{1}\right] \\ $$$${x}+{y}+{z} \\ $$$$=\sqrt{{a}^{\mathrm{2}} +\left({b}−\mathrm{1}\right)^{\mathrm{2}} }\:+\sqrt{{b}^{\mathrm{2}} +\left({c}−\mathrm{1}\right)^{\mathrm{2}} }\:+\sqrt{{c}^{\mathrm{2}} +\left({a}−\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$$$=\sqrt{\mathrm{1}+\mathrm{0}}\:+\sqrt{\mathrm{1}+\mathrm{0}}\:+\sqrt{\mathrm{1}+\mathrm{0}}\: \\ $$$$=\mathrm{3}\left({min}\:{value}\right)… \\ $$
Commented by naka3546 last updated on 19/Feb/19
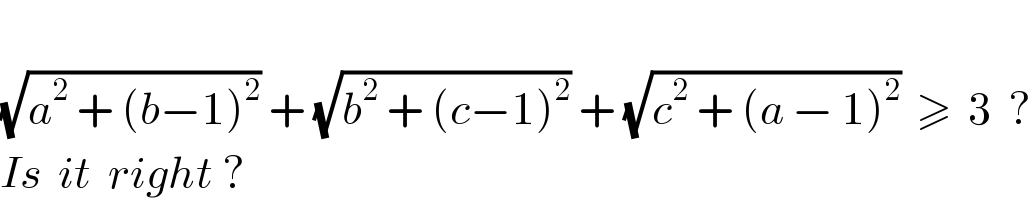
$$ \\ $$$$\sqrt{{a}^{\mathrm{2}} \:+\:\left({b}−\mathrm{1}\right)^{\mathrm{2}} }\:+\:\sqrt{{b}^{\mathrm{2}} \:+\:\left({c}−\mathrm{1}\right)^{\mathrm{2}} }\:+\:\sqrt{{c}^{\mathrm{2}} \:+\:\left({a}\:−\:\mathrm{1}\right)^{\mathrm{2}} }\:\:\geqslant\:\:\mathrm{3}\:\:? \\ $$$${Is}\:\:{it}\:\:{right}\:? \\ $$
