Question Number 55834 by Tawa1 last updated on 04/Mar/19
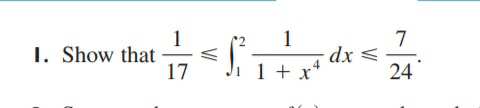
Answered by ajfour last updated on 04/Mar/19
![(2−1)f_(min) (x=2)≤∫_1 ^( 2) f(x)dx ≤ (((2−1))/2)[f(1)+f(2)] ⇒ (1/(17)) ≤∫_1 ^( 2) (dx/(1+x^4 )) ≤(1/2)((1/2)+(1/(17))) < (7/(24)) .](https://www.tinkutara.com/question/Q55839.png)
$$\:\:\:\left(\mathrm{2}−\mathrm{1}\right){f}_{{min}} \left({x}=\mathrm{2}\right)\leqslant\int_{\mathrm{1}} ^{\:\:\mathrm{2}} {f}\left({x}\right){dx}\:\leqslant\:\frac{\left(\mathrm{2}−\mathrm{1}\right)}{\mathrm{2}}\left[{f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)\right] \\ $$$$\:\:\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{17}}\:\leqslant\int_{\mathrm{1}} ^{\:\:\mathrm{2}} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{4}} }\:\leqslant\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{17}}\right)\:<\:\frac{\mathrm{7}}{\mathrm{24}}\:. \\ $$
