Question Number 58135 by rahul 19 last updated on 18/Apr/19
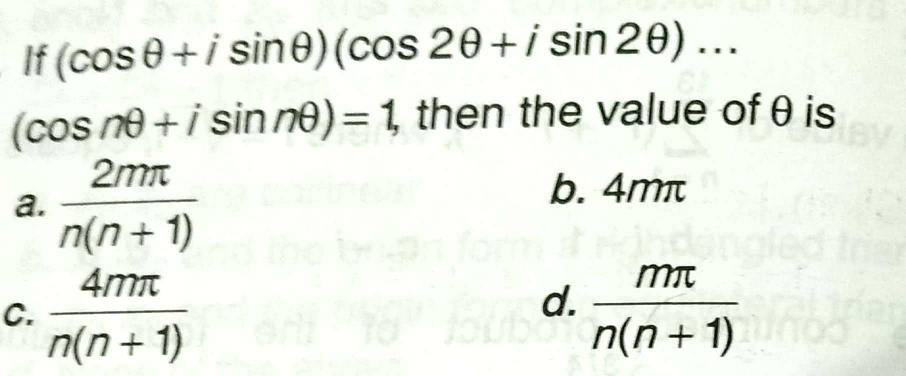
Answered by tanmay last updated on 18/Apr/19
![e^(iα) =cosα+isinα e^(iθ) ×e^(i2θ) ×e^(i3θ) ×...e^(inθ) =1=cos(2mπ+isin2mπ)=e^(i(2mπ)) e^(iθ[((n(n+1))/2)]) =e^(i(2mπ)) θ=((4mπ)/(n(n+1)))](https://www.tinkutara.com/question/Q58136.png)
$${e}^{{i}\alpha} ={cos}\alpha+{isin}\alpha \\ $$$${e}^{{i}\theta} ×{e}^{{i}\mathrm{2}\theta} ×{e}^{{i}\mathrm{3}\theta} ×…{e}^{{in}\theta} =\mathrm{1}={cos}\left(\mathrm{2}{m}\pi+{isin}\mathrm{2}{m}\pi\right)={e}^{{i}\left(\mathrm{2}{m}\pi\right)} \\ $$$${e}^{{i}\theta\left[\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\right]} ={e}^{{i}\left(\mathrm{2}{m}\pi\right)} \\ $$$$\theta=\frac{\mathrm{4}{m}\pi}{{n}\left({n}+\mathrm{1}\right)} \\ $$
Commented by rahul 19 last updated on 18/Apr/19
thanks sir!
Commented by tanmay last updated on 18/Apr/19

$${welcome}\:{rahul}… \\ $$
