Question Number 60322 by Sardor2211 last updated on 19/May/19

Commented by Mr X pcx last updated on 19/May/19
![(e)⇔xy^(′′) +y^′ =x^3 let y^′ =z ⇒ xz^′ +z =x^3 (he)⇒xz^′ +z =0 ⇒(z^′ /z) =−(1/x) ⇒ ln∣z∣ =−ln∣x∣ +k ⇒z=(c/(∣x∣)) on ]0,+∞[ ⇒z=(C/x) mvc method give z^′ =(C^′ /x) −(C/x^2 ) xz^′ +z =x^3 ⇒C^′ −(C/x) +(C/x) =x^3 ⇒ C^′ =x^3 ⇒C =(x^4 /4) +k ⇒ z(x)=(x^3 /4) +(k/x) we have y^′ =z ⇒ y =∫ zdx =∫( (x^3 /4) +(k/x))dx +λ y=(1/(16))x^4 +kln∣x∣ +λx .](https://www.tinkutara.com/question/Q60325.png)
$$\left({e}\right)\Leftrightarrow{xy}^{''} \:+{y}^{'} \:={x}^{\mathrm{3}} \:\:\:{let}\:{y}^{'} ={z}\:\Rightarrow \\ $$$${xz}^{'} \:+{z}\:={x}^{\mathrm{3}} \\ $$$$\left({he}\right)\Rightarrow{xz}^{'} \:+{z}\:=\mathrm{0}\:\Rightarrow\frac{{z}^{'} }{{z}}\:=−\frac{\mathrm{1}}{{x}}\:\Rightarrow \\ $$$${ln}\mid{z}\mid\:=−{ln}\mid{x}\mid\:+{k}\:\Rightarrow{z}=\frac{{c}}{\mid{x}\mid} \\ $$$$\left.{on}\:\right]\mathrm{0},+\infty\left[\:\Rightarrow{z}=\frac{{C}}{{x}}\:\:\:\:\:{mvc}\:{method}\:{give}\right. \\ $$$${z}^{'} \:=\frac{{C}^{'} }{{x}}\:−\frac{{C}}{{x}^{\mathrm{2}} } \\ $$$${xz}^{'} \:+{z}\:={x}^{\mathrm{3}} \:\Rightarrow{C}^{'} \:−\frac{{C}}{{x}}\:+\frac{{C}}{{x}}\:={x}^{\mathrm{3}} \:\Rightarrow \\ $$$${C}^{'} ={x}^{\mathrm{3}} \:\Rightarrow{C}\:=\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\:+{k}\:\Rightarrow\:{z}\left({x}\right)=\frac{{x}^{\mathrm{3}} }{\mathrm{4}}\:+\frac{{k}}{{x}} \\ $$$${we}\:{have}\:{y}^{'} ={z}\:\Rightarrow\:{y}\:=\int\:{zdx} \\ $$$$=\int\left(\:\frac{{x}^{\mathrm{3}} }{\mathrm{4}}\:+\frac{{k}}{{x}}\right){dx}\:+\lambda \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{16}}{x}^{\mathrm{4}} \:\:+{kln}\mid{x}\mid\:+\lambda{x}\:. \\ $$$$ \\ $$
Commented by Mr X pcx last updated on 19/May/19

$${y}=\frac{\mathrm{1}}{\mathrm{16}}{x}^{\mathrm{4}} \:+{kln}\mid{x}\mid\:+\lambda\:. \\ $$
Answered by tanmay last updated on 19/May/19
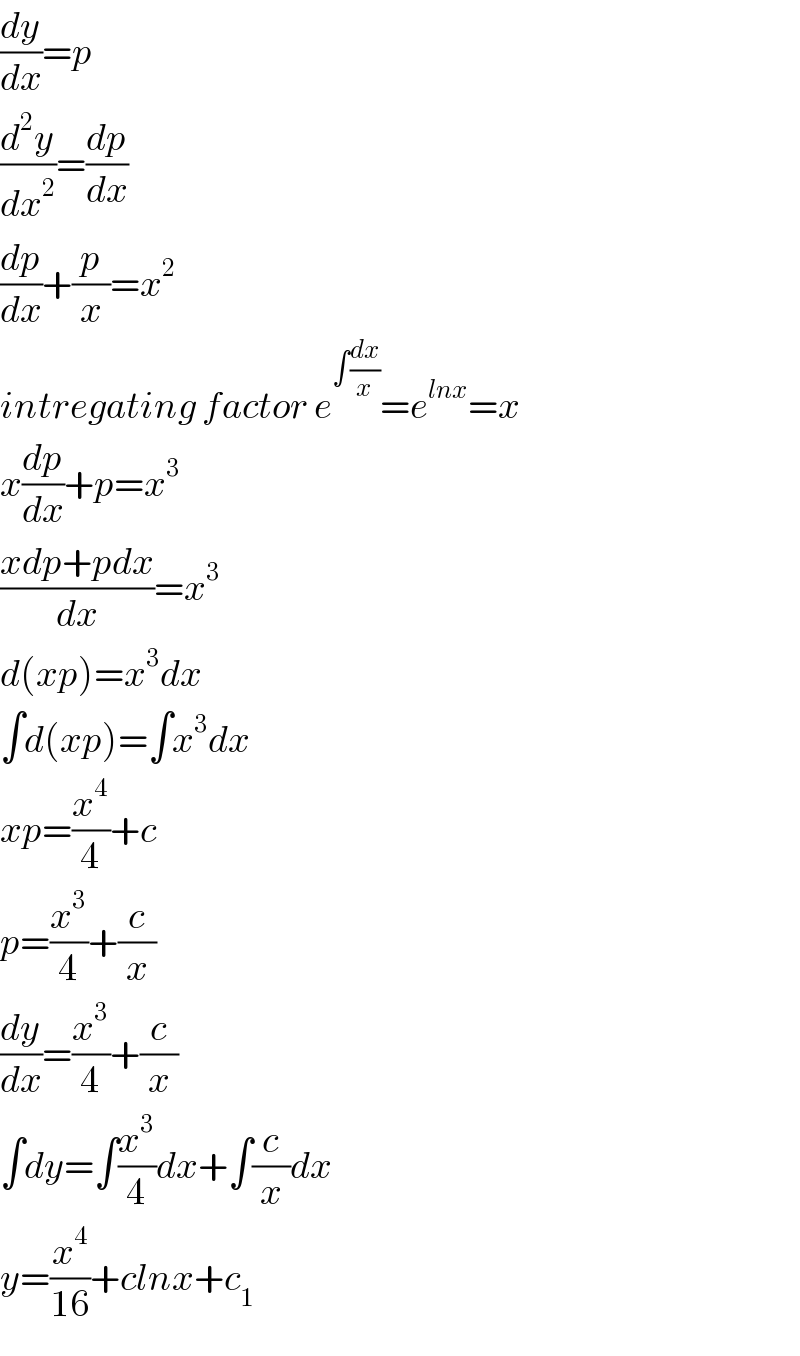
$$\frac{{dy}}{{dx}}={p} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{dp}}{{dx}} \\ $$$$\frac{{dp}}{{dx}}+\frac{{p}}{{x}}={x}^{\mathrm{2}} \\ $$$${intregating}\:{factor}\:{e}^{\int\frac{{dx}}{{x}}} ={e}^{{lnx}} ={x} \\ $$$${x}\frac{{dp}}{{dx}}+{p}={x}^{\mathrm{3}} \\ $$$$\frac{{xdp}+{pdx}}{{dx}}={x}^{\mathrm{3}} \\ $$$${d}\left({xp}\right)={x}^{\mathrm{3}} {dx} \\ $$$$\int{d}\left({xp}\right)=\int{x}^{\mathrm{3}} {dx} \\ $$$${xp}=\frac{{x}^{\mathrm{4}} }{\mathrm{4}}+{c} \\ $$$${p}=\frac{{x}^{\mathrm{3}} }{\mathrm{4}}+\frac{{c}}{{x}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{x}^{\mathrm{3}} }{\mathrm{4}}+\frac{{c}}{{x}} \\ $$$$\int{dy}=\int\frac{{x}^{\mathrm{3}} }{\mathrm{4}}{dx}+\int\frac{{c}}{{x}}{dx} \\ $$$${y}=\frac{{x}^{\mathrm{4}} }{\mathrm{16}}+{clnx}+{c}_{\mathrm{1}} \\ $$
