Question Number 61521 by necx1 last updated on 03/Jun/19

Answered by ajfour last updated on 04/Jun/19
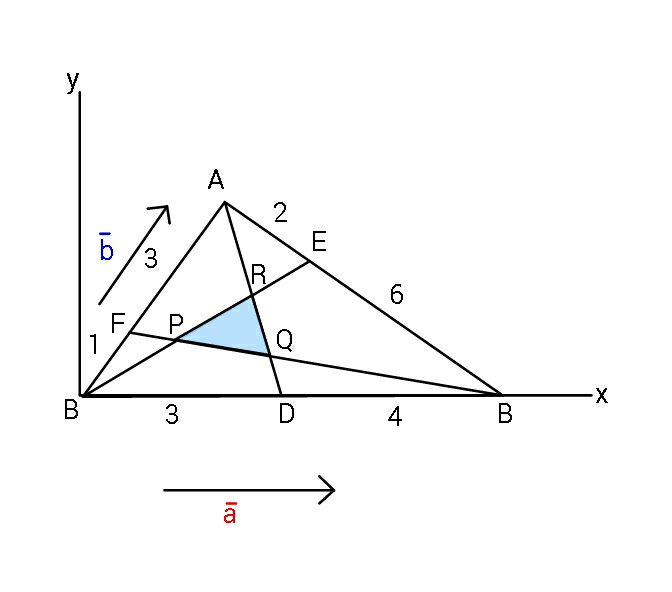
Commented by ajfour last updated on 04/Jun/19
![FB line=(b/4)+λ(a−(b/4)) BE line=μ((a/4)+((3b)/4)) r_P =(b/4)+λ(a−(b/4))=μ((a/4)+((3b)/4)) ⇒ 4λ=μ & 1−λ=3μ ⇒ λ=(1/(13)) , μ=(4/(13)) ⇒ r_P =BP = ((a+3b)/(13)) .......(i) AD=b+ρ(((3a)/7)−b) r_Q = (b/4)+λ_1 (a−(b/4))=b+ρ(((3a)/7)−b) ⇒ 4−4ρ=1−λ_1 and λ_1 =((3ρ)/7) ⇒ ρ=((21)/(25)) , λ_1 =(9/(25)) r_Q =((4b+9a)/(25)) .....(ii) r_R =μ_1 ((a/4)+((3b)/4))=b+ρ_1 (((3a)/7)−b) ⇒ μ_1 =((12)/7)ρ_1 ; 4−4ρ_1 =3μ_1 ⇒ 12−7μ_1 =9μ_1 ⇒ μ_1 =(3/4), ρ_1 =(7/(16)) r_R = ((3a)/(16))+((9b)/(16)) ....(iii) PQ=r_Q −r_P =((4b+9a)/(25))−((a+3b)/(13)) PR=r_R −r_P =((3a+9b)/(16))−((a+3b)/(13)) A_(shaded) =(1/2)∣PQ×PR∣ =(1/2)[((9/(25))−(1/(13)))((9/(16))−(3/(13)))−((4/(25))−(3/(13)))((3/(16))−(1/(13)))]∣a×b∣ =[((92)/(25×13))×((69)/(16×13))+((23)/(25×13))×((23)/(16×13))]△_(ABC) =[((92×69+23×23)/(25×16×169))]△_(ABC) A_(shaded) = ((529)/(5200))△_(ABC) ≈ 10.173%. △_(ABC) =(√(((19)/2)(((19)/2)−7)(((19)/2)−4)(((19)/2)−8))) =((√(19×5×11×3))/4) Area_(shaded) =((529)/(5200))×((√(3135))/4) A_(shaded) =((529(√(3135)))/(20800)) ≈ 1.424004](https://www.tinkutara.com/question/Q61578.png)
$${FB}\:{line}=\frac{{b}}{\mathrm{4}}+\lambda\left({a}−\frac{{b}}{\mathrm{4}}\right) \\ $$$${BE}\:{line}=\mu\left(\frac{{a}}{\mathrm{4}}+\frac{\mathrm{3}{b}}{\mathrm{4}}\right) \\ $$$${r}_{{P}} =\frac{{b}}{\mathrm{4}}+\lambda\left({a}−\frac{{b}}{\mathrm{4}}\right)=\mu\left(\frac{{a}}{\mathrm{4}}+\frac{\mathrm{3}{b}}{\mathrm{4}}\right) \\ $$$$\Rightarrow\:\:\mathrm{4}\lambda=\mu\:\:\&\:\:\:\:\mathrm{1}−\lambda=\mathrm{3}\mu \\ $$$$\Rightarrow\:\:\lambda=\frac{\mathrm{1}}{\mathrm{13}}\:\:,\:\:\mu=\frac{\mathrm{4}}{\mathrm{13}} \\ $$$$\Rightarrow\:\:\:{r}_{{P}} ={BP}\:=\:\frac{{a}+\mathrm{3}{b}}{\mathrm{13}}\:\:\:\:…….\left({i}\right) \\ $$$${AD}={b}+\rho\left(\frac{\mathrm{3}{a}}{\mathrm{7}}−{b}\right) \\ $$$${r}_{{Q}} =\:\frac{{b}}{\mathrm{4}}+\lambda_{\mathrm{1}} \left({a}−\frac{{b}}{\mathrm{4}}\right)={b}+\rho\left(\frac{\mathrm{3}{a}}{\mathrm{7}}−{b}\right) \\ $$$$\Rightarrow\:\:\mathrm{4}−\mathrm{4}\rho=\mathrm{1}−\lambda_{\mathrm{1}} \\ $$$${and}\:\:\:\:\lambda_{\mathrm{1}} =\frac{\mathrm{3}\rho}{\mathrm{7}}\:\: \\ $$$$\Rightarrow\:\:\:\rho=\frac{\mathrm{21}}{\mathrm{25}}\:\:\:,\:\:\:\lambda_{\mathrm{1}} =\frac{\mathrm{9}}{\mathrm{25}} \\ $$$$\:\:\:\:\:{r}_{{Q}} =\frac{\mathrm{4}{b}+\mathrm{9}{a}}{\mathrm{25}}\:\:\:\:\:…..\left({ii}\right) \\ $$$${r}_{{R}} =\mu_{\mathrm{1}} \left(\frac{{a}}{\mathrm{4}}+\frac{\mathrm{3}{b}}{\mathrm{4}}\right)={b}+\rho_{\mathrm{1}} \left(\frac{\mathrm{3}{a}}{\mathrm{7}}−{b}\right) \\ $$$$\Rightarrow\:\:\mu_{\mathrm{1}} =\frac{\mathrm{12}}{\mathrm{7}}\rho_{\mathrm{1}} \:\:\:\:\:;\:\:\:\mathrm{4}−\mathrm{4}\rho_{\mathrm{1}} =\mathrm{3}\mu_{\mathrm{1}} \\ $$$$\Rightarrow\:\:\mathrm{12}−\mathrm{7}\mu_{\mathrm{1}} =\mathrm{9}\mu_{\mathrm{1}} \\ $$$$\Rightarrow\:\:\:\:\:\mu_{\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{4}},\:\:\:\rho_{\mathrm{1}} =\frac{\mathrm{7}}{\mathrm{16}} \\ $$$${r}_{{R}} =\:\frac{\mathrm{3}{a}}{\mathrm{16}}+\frac{\mathrm{9}{b}}{\mathrm{16}}\:\:\:\:\:\:….\left({iii}\right) \\ $$$${PQ}={r}_{{Q}} −{r}_{{P}} =\frac{\mathrm{4}{b}+\mathrm{9}{a}}{\mathrm{25}}−\frac{{a}+\mathrm{3}{b}}{\mathrm{13}} \\ $$$${PR}={r}_{{R}} −{r}_{{P}} =\frac{\mathrm{3}{a}+\mathrm{9}{b}}{\mathrm{16}}−\frac{{a}+\mathrm{3}{b}}{\mathrm{13}} \\ $$$${A}_{{shaded}} =\frac{\mathrm{1}}{\mathrm{2}}\mid{PQ}×{PR}\mid \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\frac{\mathrm{9}}{\mathrm{25}}−\frac{\mathrm{1}}{\mathrm{13}}\right)\left(\frac{\mathrm{9}}{\mathrm{16}}−\frac{\mathrm{3}}{\mathrm{13}}\right)−\left(\frac{\mathrm{4}}{\mathrm{25}}−\frac{\mathrm{3}}{\mathrm{13}}\right)\left(\frac{\mathrm{3}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{13}}\right)\right]\mid{a}×{b}\mid \\ $$$$\:\:\:=\left[\frac{\mathrm{92}}{\mathrm{25}×\mathrm{13}}×\frac{\mathrm{69}}{\mathrm{16}×\mathrm{13}}+\frac{\mathrm{23}}{\mathrm{25}×\mathrm{13}}×\frac{\mathrm{23}}{\mathrm{16}×\mathrm{13}}\right]\bigtriangleup_{{ABC}} \\ $$$$\:\:=\left[\frac{\mathrm{92}×\mathrm{69}+\mathrm{23}×\mathrm{23}}{\mathrm{25}×\mathrm{16}×\mathrm{169}}\right]\bigtriangleup_{{ABC}} \\ $$$$\:{A}_{{shaded}} \:=\:\frac{\mathrm{529}}{\mathrm{5200}}\bigtriangleup_{{ABC}} \:\:\approx\:\mathrm{10}.\mathrm{173\%}. \\ $$$$\bigtriangleup_{{ABC}} =\sqrt{\frac{\mathrm{19}}{\mathrm{2}}\left(\frac{\mathrm{19}}{\mathrm{2}}−\mathrm{7}\right)\left(\frac{\mathrm{19}}{\mathrm{2}}−\mathrm{4}\right)\left(\frac{\mathrm{19}}{\mathrm{2}}−\mathrm{8}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{19}×\mathrm{5}×\mathrm{11}×\mathrm{3}}}{\mathrm{4}} \\ $$$${Area}_{{shaded}} =\frac{\mathrm{529}}{\mathrm{5200}}×\frac{\sqrt{\mathrm{3135}}}{\mathrm{4}} \\ $$$$\:\boldsymbol{{A}}_{{shaded}} \:=\frac{\mathrm{529}\sqrt{\mathrm{3135}}}{\mathrm{20800}}\:\approx\:\mathrm{1}.\mathrm{424004}\: \\ $$
Commented by Tawa1 last updated on 05/Jun/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
