Menu Close

Question-63410

Tinku Tara 0 Comments
Pin




Question Number 63410 by aliesam last updated on 03/Jul/19
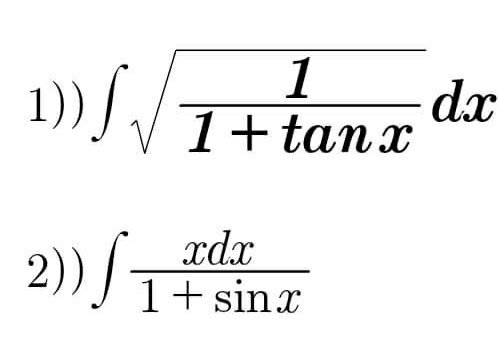
Commented by mathmax by abdo last updated on 03/Jul/19
2) let I =∫ ((xdx)/(1+sinx)) changement tan((x/2))=t give I = ∫ ((2arctan(t))/((1+((2t)/(1+t^2 )))(1+t^2 )))dt = 2∫ ((arctan(t))/(1+t^2 +2t)) dt =2 ∫ ((arctan(t))/((t+1)^2 )) dt =_(by pwrts) 2{ −((arcant)/(t+1)) −∫ −(1/(t+1)) (dt/(1+t^2 ))} −((2 arctan(t))/(t+1)) + 2 ∫ (dt/((t+1)(t^2 +1))) let decompose F(t) =(1/((t+1)(t^2 +1))) ⇒F(t) =(a/(t+1)) +((bt +c)/(t^2 +1)) a =lim_(t→−1) (t+1)F(t) =(1/2) lim_(t→+∞) t F(t) =0 =a+b ⇒b=−(1/2) ⇒F(t)=(1/(2(t+1))) −(1/2) ((t −2c)/(t^2 +1)) F(0) =1 =(1/2) +c ⇒c=(1/2) ⇒F(t)=(1/(2(t+1))) −(1/2) ((t−1)/(t^2 +1)) ⇒ ∫ (dt/((t+1)(t^2 +1))) = ∫ (dt/(2(t+1))) −(1/4) ∫ ((2t)/(t^2 +1)) +(1/2) ∫ (dt/(t^2 +1)) =(1/2)ln∣t+1∣−(1/4)ln(t^2 +1)+(1/2) arctan(t)+c =(1/2)ln∣1+tan((x/2))∣−(1/4)ln(1+tan^2 ((x/2))) +x +c ⇒ I =−(x/(1+tan((x/2)))) +ln∣1+tan((x/2))∣−(1/2)ln(1+tan^2 ((x/2))) +x +c .
$$\left.\mathrm{2}\right)\:{let}\:{I}\:=\int\:\:\:\frac{{xdx}}{\mathrm{1}+{sinx}}\:\:\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\: \\ $$$${I}\:=\:\int\:\:\:\frac{\mathrm{2}{arctan}\left({t}\right)}{\left(\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}\:=\:\mathrm{2}\int\:\:\:\:\frac{{arctan}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}}\:{dt}\:=\mathrm{2}\:\int\:\:\:\frac{{arctan}\left({t}\right)}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:{dt}\:\: \\ $$$$=_{{by}\:{pwrts}} \:\:\:\:\mathrm{2}\left\{\:\:\:−\frac{{arcant}}{{t}+\mathrm{1}}\:−\int\:\:−\frac{\mathrm{1}}{{t}+\mathrm{1}}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right\} \\ $$$$−\frac{\mathrm{2}\:{arctan}\left({t}\right)}{{t}+\mathrm{1}}\:+\:\mathrm{2}\:\int\:\:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:{let}\:{decompose} \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{1}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow{F}\left({t}\right)\:=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{bt}\:+{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow−\mathrm{1}} \left({t}+\mathrm{1}\right){F}\left({t}\right)\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)\:=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}=−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\:\frac{{t}\:−\mathrm{2}{c}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{1}\:=\frac{\mathrm{1}}{\mathrm{2}}\:+{c}\:\Rightarrow{c}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{t}−\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\:\int\:\:\frac{{dt}}{\mathrm{2}\left({t}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{4}}\:\int\:\:\frac{\mathrm{2}{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{t}+\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}\:{arctan}\left({t}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\:+{x}\:+{c}\:\:\Rightarrow \\ $$$${I}\:=−\frac{{x}}{\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\:+{ln}\mid\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\:+{x}\:+{c}\:. \\ $$
Commented by aliesam last updated on 04/Jul/19
perfect
$${perfect} \\ $$
Answered by MJS last updated on 04/Jul/19
2) ∫(x/(1+sin x))dx by parts u′=(1/(1+sin x)) → u=∫(dx/(1+sin x)) v=x → v′=1 ∫u′v=uv−∫uv′ ∫(x/(1+sin x))dx=x∫(dx/(1+sin x))−∫(∫(dx/(1+sin x)))dx ∫(dx/(1+sin x))= [t=tan (x/2) → dx=2cos^2 (x/2) dt] =2∫(dt/((t+1)^2 ))=−(2/(t+1))=−2((cos (x/2))/(cos (x/2) +sin (x/2)))= =tan x −(1/(cos x))−1 ∫(∫(dx/(1+sin x)))dx=∫tan x dx−∫(dx/(cos x))−∫dx= =−ln cos x −ln ((cos x)/(1−sin x)) −x=−x+ln (1/(1+sin x)) ⇒ ∫(x/(1+sin x))dx=xtan x −(x/(cos x))−x+x−ln (1/(1+sin x)) = =xtan x −(x/(cos x))−ln (1/(1+sin x)) +C
$$\left.\mathrm{2}\right) \\ $$$$\int\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx} \\ $$$$\mathrm{by}\:\mathrm{parts} \\ $$$${u}'=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}}\:\rightarrow\:{u}=\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}} \\ $$$${v}={x}\:\rightarrow\:{v}'=\mathrm{1} \\ $$$$\int{u}'{v}={uv}−\int{uv}' \\ $$$$\int\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx}={x}\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}}−\int\left(\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}}\right){dx} \\ $$$$\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\mathrm{2cos}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\:{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\mathrm{2}}{{t}+\mathrm{1}}=−\mathrm{2}\frac{\mathrm{cos}\:\frac{{x}}{\mathrm{2}}}{\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\:+\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}= \\ $$$$=\mathrm{tan}\:{x}\:−\frac{\mathrm{1}}{\mathrm{cos}\:{x}}−\mathrm{1} \\ $$$$\int\left(\int\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}}\right){dx}=\int\mathrm{tan}\:{x}\:{dx}−\int\frac{{dx}}{\mathrm{cos}\:{x}}−\int{dx}= \\ $$$$=−\mathrm{ln}\:\mathrm{cos}\:{x}\:−\mathrm{ln}\:\frac{\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}}\:−{x}=−{x}+\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}} \\ $$$$\Rightarrow \\ $$$$\int\frac{{x}}{\mathrm{1}+\mathrm{sin}\:{x}}{dx}={x}\mathrm{tan}\:{x}\:−\frac{{x}}{\mathrm{cos}\:{x}}−{x}+{x}−\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}}\:= \\ $$$$={x}\mathrm{tan}\:{x}\:−\frac{{x}}{\mathrm{cos}\:{x}}−\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{x}}\:+{C} \\ $$
Answered by MJS last updated on 04/Jul/19
1) ∫(dx/( (√(1+tan x))))= [t=(√(1+tan x)) → dx=((2t)/(t^4 −2t^2 +2))dt] =2∫(dt/(t^4 −2t^2 +2))=2∫(dt/((t^2 −(√(2+2(√2)))t+(√2))(t^2 +(√(2+2(√2)))t+(√2))))= (√(2+2(√2)))=a (√2)=b =2∫(dt/((t^2 −at+b)(t^2 +at+b)))= =−(1/(ab))∫((t−a)/(t^2 −at+b))dt+(1/(ab))∫((t+a)/(t^2 +at+b))dt= =−(1/(2ab))∫((2t−a)/(t^2 −at+b))dt+(1/(2b))∫(dt/(t^2 −at+b))+(1/(2ab))∫((2t+a)/(t^2 +at+b))dt+(1/(2b))∫(dt/(t^2 +at+b))= =−(1/(2ab))ln (t^2 −at+b) +(1/(b(√(4b−a^2 ))))arctan ((2t−a)/( (√(4b−a^2 )))) +(1/(2ab))ln (t^2 +at+b) +(1/(b(√(4b−a^2 ))))arctan ((2t+a)/( (√(4b−a^2 )))) = =(1/(2ab))ln ((t^2 +at+b)/(t^2 −at+b)) +(1/(b(√(4b−a^2 ))))(arctan ((2t−a)/( (√(4b−a^2 )))) +arctan ((2t+a)/( (√(4b−a^2 ))))) ...
$$\left.\mathrm{1}\right) \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{1}+\mathrm{tan}\:{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{1}+\mathrm{tan}\:{x}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{t}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}}=\mathrm{2}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{t}+\sqrt{\mathrm{2}}\right)\left({t}^{\mathrm{2}} +\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}{t}+\sqrt{\mathrm{2}}\right)}= \\ $$$$\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{2}}}={a} \\ $$$$\sqrt{\mathrm{2}}={b} \\ $$$$=\mathrm{2}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −{at}+{b}\right)\left({t}^{\mathrm{2}} +{at}+{b}\right)}= \\ $$$$=−\frac{\mathrm{1}}{{ab}}\int\frac{{t}−{a}}{{t}^{\mathrm{2}} −{at}+{b}}{dt}+\frac{\mathrm{1}}{{ab}}\int\frac{{t}+{a}}{{t}^{\mathrm{2}} +{at}+{b}}{dt}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{ab}}\int\frac{\mathrm{2}{t}−{a}}{{t}^{\mathrm{2}} −{at}+{b}}{dt}+\frac{\mathrm{1}}{\mathrm{2}{b}}\int\frac{{dt}}{{t}^{\mathrm{2}} −{at}+{b}}+\frac{\mathrm{1}}{\mathrm{2}{ab}}\int\frac{\mathrm{2}{t}+{a}}{{t}^{\mathrm{2}} +{at}+{b}}{dt}+\frac{\mathrm{1}}{\mathrm{2}{b}}\int\frac{{dt}}{{t}^{\mathrm{2}} +{at}+{b}}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{ab}}\mathrm{ln}\:\left({t}^{\mathrm{2}} −{at}+{b}\right)\:+\frac{\mathrm{1}}{{b}\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\mathrm{arctan}\:\frac{\mathrm{2}{t}−{a}}{\:\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\:+\frac{\mathrm{1}}{\mathrm{2}{ab}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +{at}+{b}\right)\:+\frac{\mathrm{1}}{{b}\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\mathrm{arctan}\:\frac{\mathrm{2}{t}+{a}}{\:\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{ab}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} +{at}+{b}}{{t}^{\mathrm{2}} −{at}+{b}}\:+\frac{\mathrm{1}}{{b}\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\left(\mathrm{arctan}\:\frac{\mathrm{2}{t}−{a}}{\:\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\:+\mathrm{arctan}\:\frac{\mathrm{2}{t}+{a}}{\:\sqrt{\mathrm{4}{b}−{a}^{\mathrm{2}} }}\right) \\ $$$$… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *