Question-64971

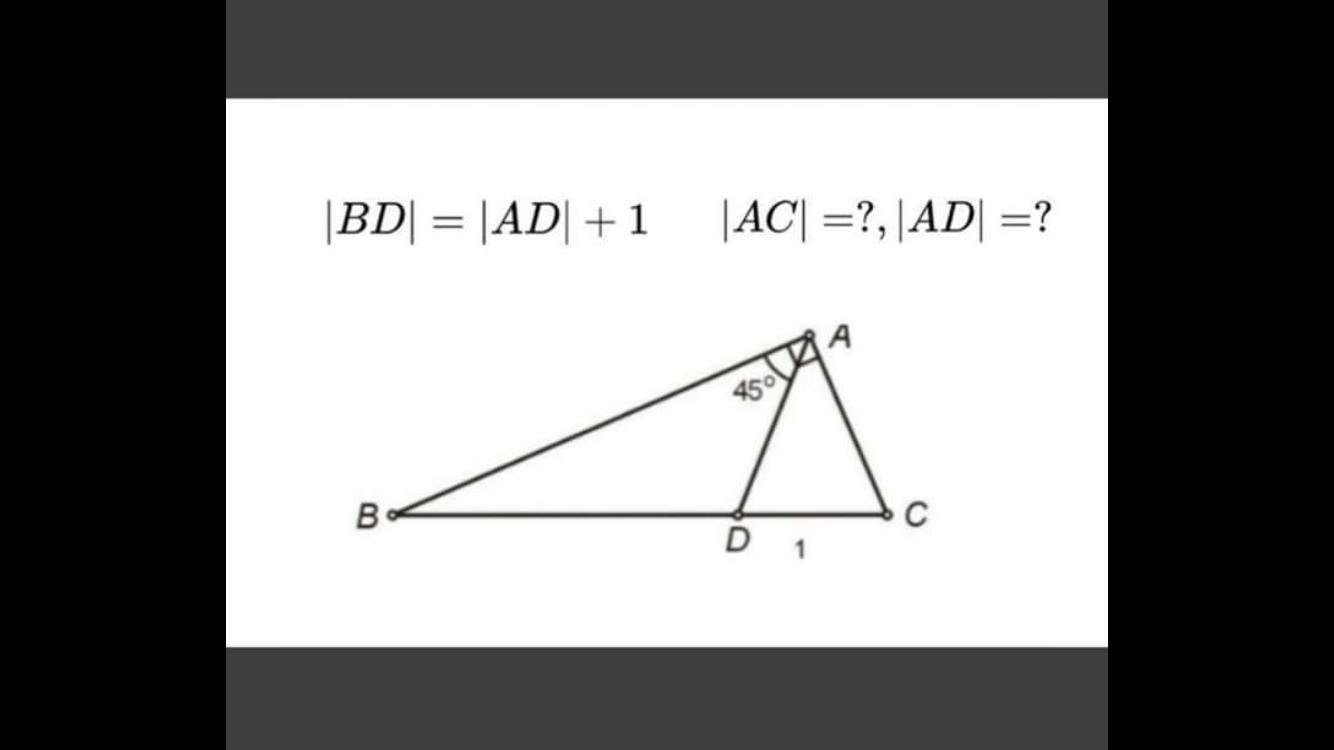
Question Number 64971 by Tawa1 last updated on 23/Jul/19

Commented by Tony Lin last updated on 23/Jul/19

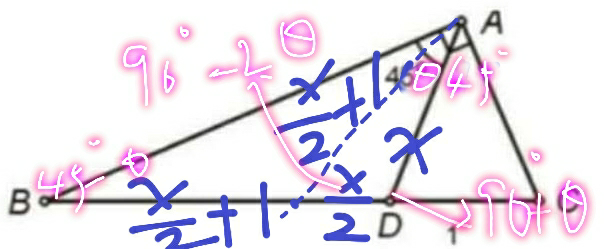
((x/2)/(sinθ))=(((x/2)+1)/(sin(90°+θ)))=(x/(sin(90°−2θ))) ⇒((x/2)/(sinθ))=(((x/2)+1)/(cosθ))=(x/(cos2θ)) let cosθ=t ⇒((x/2)/( (√(1−t^2 ))))=(((x/2)+1)/t)=(x/(2t^2 −1)) (t/( (√(1−t^2 ))))=(((x/2)+1)/(x/2))=1+(2/x)→(1) (t^2 /(1−t^2 ))=(1+(2/x))^2 t^2 =(1+(2/x))^2 −(1+(2/x))^2 t^2 [(1+(2/x))^2 +1]t^2 =(1+(2/x))^2 ⇒t^2 =(((1+(2/x))^2 )/((1+(2/x))^2 +1)) ((x/2)/( (√(1−t^2 ))))=(x/(2t^2 −1))→(2) 2(√(1−t^2 ))=2t^2 −1 4(1−t^2 )=4t^4 −4t^2 +1 ⇒t^2 =((√3)/2) from (1)&(2) ⇒((√3)/2)=(((1+(2/x))^2 )/((1+(2/x))^2 +1)) (√3)=(2−(√3))(1+(2/x))^2 (1+(2/x))^2 =((√3)/(2−(√3))) ⇒x=AD=(2/( (√((√3)/(2−(√3))))−1))≒1.297 AC=(√(AD^2 +1−2ADcos(90°−θ))) =(√(AD^2 +1−2ADsinθ)) ≒1.316 please check if there are any mistakes

$$\frac{\frac{{x}}{\mathrm{2}}}{{sin}\theta}=\frac{\frac{{x}}{\mathrm{2}}+\mathrm{1}}{{sin}\left(\mathrm{90}°+\theta\right)}=\frac{{x}}{{sin}\left(\mathrm{90}°−\mathrm{2}\theta\right)} \\ $$$$\Rightarrow\frac{\frac{{x}}{\mathrm{2}}}{{sin}\theta}=\frac{\frac{{x}}{\mathrm{2}}+\mathrm{1}}{{cos}\theta}=\frac{{x}}{{cos}\mathrm{2}\theta} \\ $$$${let}\:{cos}\theta={t} \\ $$$$\Rightarrow\frac{\frac{{x}}{\mathrm{2}}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\frac{\frac{{x}}{\mathrm{2}}+\mathrm{1}}{{t}}=\frac{{x}}{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\frac{\frac{{x}}{\mathrm{2}}+\mathrm{1}}{\frac{{x}}{\mathrm{2}}}=\mathrm{1}+\frac{\mathrm{2}}{{x}}\rightarrow\left(\mathrm{1}\right) \\ $$$$\frac{{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }=\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} \\ $$$${t}^{\mathrm{2}} =\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} −\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} {t}^{\mathrm{2}} \\ $$$$\left[\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}\right]{t}^{\mathrm{2}} =\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{t}^{\mathrm{2}} =\frac{\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\frac{\frac{{x}}{\mathrm{2}}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}=\frac{{x}}{\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1}}\rightarrow\left(\mathrm{2}\right) \\ $$$$\mathrm{2}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }=\mathrm{2}{t}^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{4}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)=\mathrm{4}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1} \\ $$$$\Rightarrow{t}^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${from}\:\left(\mathrm{1}\right)\&\left(\mathrm{2}\right) \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$\sqrt{\mathrm{3}}=\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{x}={AD}=\frac{\mathrm{2}}{\:\sqrt{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}−\sqrt{\mathrm{3}}}}−\mathrm{1}}\fallingdotseq\mathrm{1}.\mathrm{297} \\ $$$${AC}=\sqrt{{AD}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{ADcos}\left(\mathrm{90}°−\theta\right)} \\ $$$$\:\:\:\:\:\:\:=\sqrt{{AD}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{ADsin}\theta} \\ $$$$\:\:\:\:\:\:\:\fallingdotseq\mathrm{1}.\mathrm{316} \\ $$$${please}\:{check}\:{if}\:{there}\:{are}\:{any}\:{mistakes} \\ $$

Commented by Tony Lin last updated on 23/Jul/19