Question Number 83032 by Power last updated on 27/Feb/20
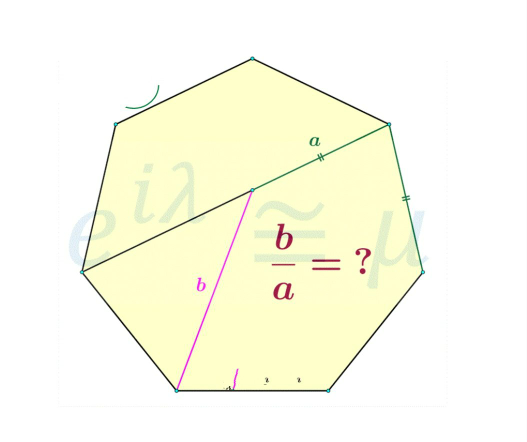
Answered by mr W last updated on 27/Feb/20
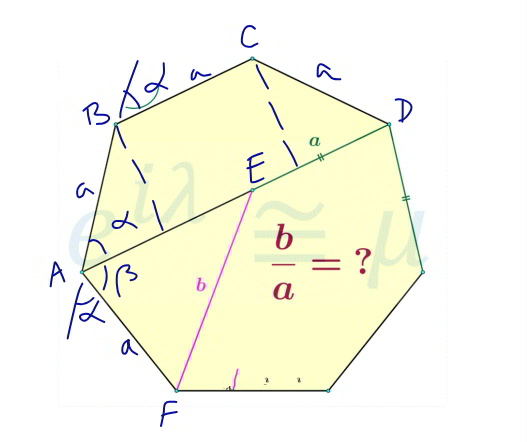
Commented by mr W last updated on 27/Feb/20
![α=((360°)/7)=((2π)/7) β=180−2α AD=a+2a cos α AE=AD−a=2a cos α b^2 =a^2 +(2a cos α)^2 −2a(2a cos α) cos β =a^2 +4a^2 cos^2 α+4a^2 cos α cos 2α =a^2 [3+2 cos 2α (1+2 cos α)] b=a(√(3+2 cos 2α (1+2 cos α))) ⇒(b/a)=(√(3−2 cos ((3π)/7) (1+2 cos ((2π)/7))))=(√2)](https://www.tinkutara.com/question/Q83058.png)
$$\alpha=\frac{\mathrm{360}°}{\mathrm{7}}=\frac{\mathrm{2}\pi}{\mathrm{7}} \\ $$$$\beta=\mathrm{180}−\mathrm{2}\alpha \\ $$$${AD}={a}+\mathrm{2}{a}\:\mathrm{cos}\:\alpha \\ $$$${AE}={AD}−{a}=\mathrm{2}{a}\:\mathrm{cos}\:\alpha \\ $$$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} +\left(\mathrm{2}{a}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} −\mathrm{2}{a}\left(\mathrm{2}{a}\:\mathrm{cos}\:\alpha\right)\:\mathrm{cos}\:\beta \\ $$$$={a}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\alpha+\mathrm{4}{a}^{\mathrm{2}} \:\mathrm{cos}\:\alpha\:\mathrm{cos}\:\mathrm{2}\alpha \\ $$$$={a}^{\mathrm{2}} \left[\mathrm{3}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\alpha\:\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\alpha\right)\right] \\ $$$${b}={a}\sqrt{\mathrm{3}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\alpha\:\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\alpha\right)} \\ $$$$\Rightarrow\frac{{b}}{{a}}=\sqrt{\mathrm{3}−\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{3}\pi}{\mathrm{7}}\:\left(\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\frac{\mathrm{2}\pi}{\mathrm{7}}\right)}=\sqrt{\mathrm{2}} \\ $$
Commented by Power last updated on 27/Feb/20
$$\mathrm{great}\:\mathrm{sir}\:\mathrm{thank}\:\mathrm{you} \\ $$
