Question Number 87911 by jagoll last updated on 07/Apr/20
Commented by jagoll last updated on 07/Apr/20

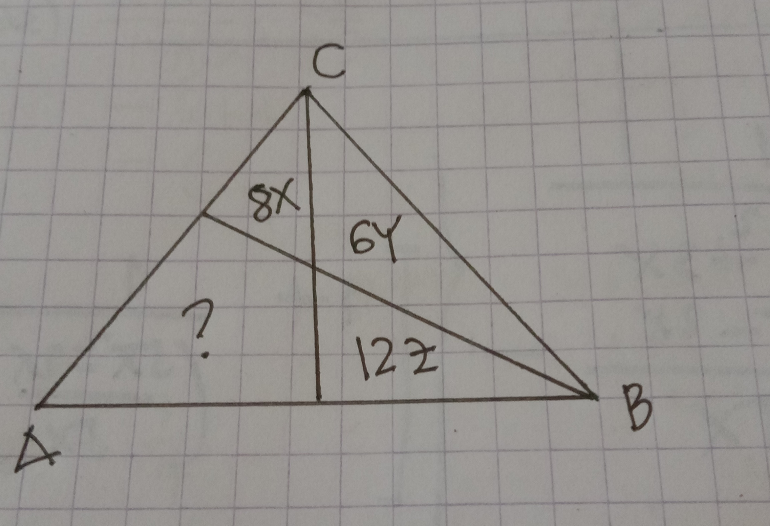
$$\mathrm{dear}\:\mathrm{mr}\:\mathrm{W}. \\ $$$$\mathrm{i}\:\mathrm{forgot}\:\mathrm{your}\:\mathrm{method}. \\ $$$$\mathrm{please}\:\mathrm{remember}\:\mathrm{me}\:\mathrm{for}\:\mathrm{this}\: \\ $$$$\mathrm{question} \\ $$
Commented by john santu last updated on 07/Apr/20
![(t_1 /(8x)) = ((t_2 +12z)/(6y)) ((t_1 +8x)/(6y)) = (t_2 /(12z)) [ let 8x = a , 6y = b , 12z = c ] ⇒t_1 = (a/b)(t_2 +c ) (i) ⇒t_1 + a = (b/c)t_2 , t_1 = ((bt_2 )/c) − a (ii) (a/b)(t_2 +c) = (b/c)t_2 −a t_2 ((a/b) − (b/c)) = −a−((ac)/b) t_2 (((b^2 −ac)/(bc))) = ((a(b+c))/b) t_2 = ((ac(b+c))/(b^2 −ac)). now t_1 = ((bt_2 −ac)/c) = (((((abc(b+c))/(b^2 −ac)))−ac)/c) t_1 = ((ab^2 c+abc^2 −ab^2 c+(ac)^2 )/(c(b^2 −ac))) t_1 = ((ac^2 (b+a))/(c(b^2 −ac))) the area we required = t_1 +t_2 = ((ac^2 (a+b))/(c(b^2 −ac))) + ((ac(b+c))/(b^2 −ac)) = ((ac^2 (a+2b+c))/(c(b^2 −ac))) = ((ac(a+2b+c))/(b^2 −ac))](https://www.tinkutara.com/question/Q87913.png)
$$\frac{\mathrm{t}_{\mathrm{1}} }{\mathrm{8x}}\:=\:\frac{\mathrm{t}_{\mathrm{2}} +\mathrm{12z}}{\mathrm{6y}} \\ $$$$\frac{\mathrm{t}_{\mathrm{1}} +\mathrm{8x}}{\mathrm{6y}}\:=\:\frac{\mathrm{t}_{\mathrm{2}} }{\mathrm{12z}}\: \\ $$$$\left[\:\mathrm{let}\:\mathrm{8x}\:=\:\mathrm{a}\:,\:\mathrm{6y}\:=\:\mathrm{b}\:,\:\mathrm{12z}\:=\:\mathrm{c}\:\right] \\ $$$$\Rightarrow\mathrm{t}_{\mathrm{1}} \:=\:\frac{\mathrm{a}}{\mathrm{b}}\left(\mathrm{t}_{\mathrm{2}} +\mathrm{c}\:\right)\:\left(\mathrm{i}\right) \\ $$$$\Rightarrow\mathrm{t}_{\mathrm{1}} +\:\mathrm{a}\:=\:\frac{\mathrm{b}}{\mathrm{c}}\mathrm{t}_{\mathrm{2}} \:,\:\mathrm{t}_{\mathrm{1}} \:=\:\frac{\mathrm{bt}_{\mathrm{2}} }{\mathrm{c}}\:−\:\mathrm{a}\:\left(\mathrm{ii}\right) \\ $$$$\frac{\mathrm{a}}{\mathrm{b}}\left(\mathrm{t}_{\mathrm{2}} +\mathrm{c}\right)\:=\:\frac{\mathrm{b}}{\mathrm{c}}\mathrm{t}_{\mathrm{2}} \:−\mathrm{a}\: \\ $$$$\mathrm{t}_{\mathrm{2}} \left(\frac{\mathrm{a}}{\mathrm{b}}\:−\:\frac{\mathrm{b}}{\mathrm{c}}\right)\:=\:−\mathrm{a}−\frac{\mathrm{ac}}{\mathrm{b}} \\ $$$$\mathrm{t}_{\mathrm{2}} \left(\frac{\mathrm{b}^{\mathrm{2}} −\mathrm{ac}}{\mathrm{bc}}\right)\:=\:\frac{\mathrm{a}\left(\mathrm{b}+\mathrm{c}\right)}{\mathrm{b}} \\ $$$$\mathrm{t}_{\mathrm{2}} \:=\:\frac{\mathrm{ac}\left(\mathrm{b}+\mathrm{c}\right)}{\mathrm{b}^{\mathrm{2}} −\mathrm{ac}}.\:\mathrm{now}\: \\ $$$$\mathrm{t}_{\mathrm{1}} \:=\:\frac{\mathrm{bt}_{\mathrm{2}} −\mathrm{ac}}{\mathrm{c}}\:=\:\frac{\left(\frac{\mathrm{abc}\left(\mathrm{b}+\mathrm{c}\right)}{\mathrm{b}^{\mathrm{2}} −\mathrm{ac}}\right)−\mathrm{ac}}{\mathrm{c}} \\ $$$$\mathrm{t}_{\mathrm{1}} \:=\:\frac{\mathrm{ab}^{\mathrm{2}} \mathrm{c}+\mathrm{abc}^{\mathrm{2}} −\mathrm{ab}^{\mathrm{2}} \mathrm{c}+\left(\mathrm{ac}\right)^{\mathrm{2}} }{\mathrm{c}\left(\mathrm{b}^{\mathrm{2}} −\mathrm{ac}\right)} \\ $$$$\mathrm{t}_{\mathrm{1}} \:=\:\frac{\mathrm{ac}^{\mathrm{2}} \left(\mathrm{b}+\mathrm{a}\right)}{\mathrm{c}\left(\mathrm{b}^{\mathrm{2}} −\mathrm{ac}\right)} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{we}\:\mathrm{required}\:=\:\mathrm{t}_{\mathrm{1}} +\mathrm{t}_{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{ac}^{\mathrm{2}} \left(\mathrm{a}+\mathrm{b}\right)}{\mathrm{c}\left(\mathrm{b}^{\mathrm{2}} −\mathrm{ac}\right)}\:+\:\frac{\mathrm{ac}\left(\mathrm{b}+\mathrm{c}\right)}{\mathrm{b}^{\mathrm{2}} −\mathrm{ac}} \\ $$$$=\:\frac{\mathrm{ac}^{\mathrm{2}} \left(\mathrm{a}+\mathrm{2b}+\mathrm{c}\right)}{\mathrm{c}\left(\mathrm{b}^{\mathrm{2}} −\mathrm{ac}\right)}\:=\:\frac{\mathrm{ac}\left(\mathrm{a}+\mathrm{2b}+\mathrm{c}\right)}{\mathrm{b}^{\mathrm{2}} −\mathrm{ac}} \\ $$
Commented by jagoll last updated on 07/Apr/20
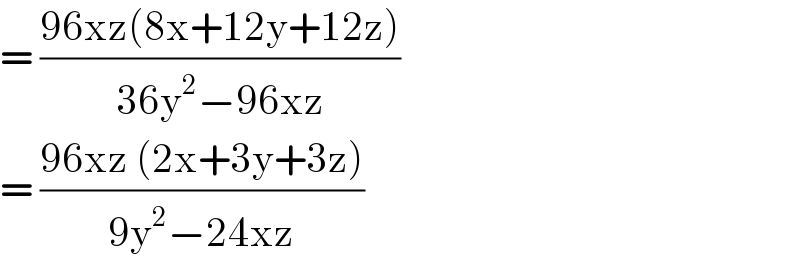
$$=\:\frac{\mathrm{96xz}\left(\mathrm{8x}+\mathrm{12y}+\mathrm{12z}\right)}{\mathrm{36y}^{\mathrm{2}} −\mathrm{96xz}} \\ $$$$=\:\frac{\mathrm{96xz}\:\left(\mathrm{2x}+\mathrm{3y}+\mathrm{3z}\right)}{\mathrm{9y}^{\mathrm{2}} −\mathrm{24xz}} \\ $$
