Question-93208

Question Number 93208 by Power last updated on 11/May/20

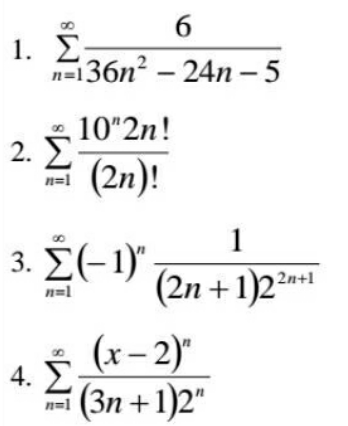
Commented by mathmax by abdo last updated on 11/May/20

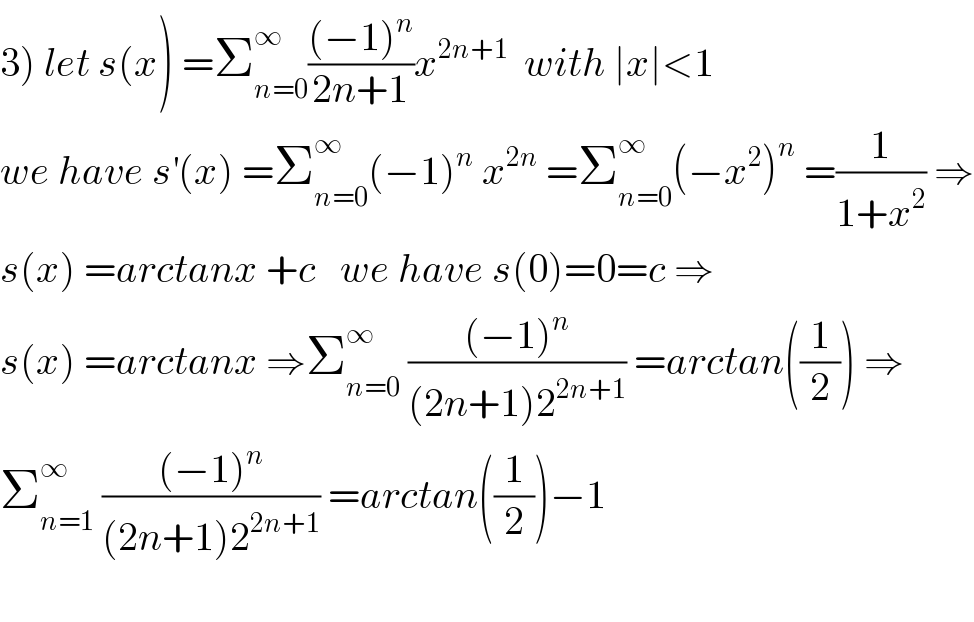
3) let s(x) =Σ_(n=0) ^∞ (((−1)^n )/(2n+1))x^(2n+1) with ∣x∣<1 we have s^′ (x) =Σ_(n=0) ^∞ (−1)^n x^(2n) =Σ_(n=0) ^∞ (−x^2 )^n =(1/(1+x^2 )) ⇒ s(x) =arctanx +c we have s(0)=0=c ⇒ s(x) =arctanx ⇒Σ_(n=0) ^∞ (((−1)^n )/((2n+1)2^(2n+1) )) =arctan((1/2)) ⇒ Σ_(n=1) ^∞ (((−1)^n )/((2n+1)2^(2n+1) )) =arctan((1/2))−1

$$\left.\mathrm{3}\right)\:{let}\:{s}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} \:\:{with}\:\mid{x}\mid<\mathrm{1} \\ $$$${we}\:{have}\:{s}^{'} \left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−{x}^{\mathrm{2}} \right)^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${s}\left({x}\right)\:={arctanx}\:+{c}\:\:\:{we}\:{have}\:{s}\left(\mathrm{0}\right)=\mathrm{0}={c}\:\Rightarrow \\ $$$${s}\left({x}\right)\:={arctanx}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\:={arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }\:={arctan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{1} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 11/May/20

4) let w(x) =Σ_(n=0) ^∞ (((x−2)^n )/((3n+1)2^n )) ⇒w(x) =Σ_(n=0) ^∞ (1/(3n+1))(((x−2)/2))^n =Σ_(n=0) ^∞ (1/(3n+1))((x/2)−1)^n =Σ_(n=0) ^∞ (t^n /(3n+1)) serie cv ⇒∣(x/2)−1∣<1 ⇒∣x−2∣<2 ⇒−2<x−2<2 ⇒0<x<4 in this case ∣t∣<1 we have Σ_(n=0) ^∞ (t^n /(3n+1)) =(1/((^3 (√t))))Σ_(n=0) ^∞ (((^3 (√t))^(3n+1) )/(3n+1)) =(1/((^3 (√t))))ϕ(^3 (√t)) with ϕ(u) =Σ_(n=0) ^∞ (u^(3n+1) /(3n+1)) ⇒ϕ^′ (u) =Σ_(n=0) ^∞ u^(3n) =(1/(1−u^3 )) ⇒ ϕ(u) =∫_0 ^u (dx/(1−x^3 )) +c (c=ϕ(0) =0) −ϕ(u) =∫_0 ^u (dx/((x−1)(x^2 +x+1))) let decompose F =(1/((x−1)(x^2 +x+1))) =(a/(x−1)) +((bx +c)/(x^2 +x+1)) a =(1/3) , lim_(x→+∞) xF (x)=0 =a+b ⇒b =−(1/3) F(0) =−1 =−a+c ⇒c=a−1 =−(2/3) ⇒ F =(1/(3(x−1))) −(1/3)×((x+2)/(x^2 +x+1)) ⇒ ∫_0 ^u F(x)dx =(1/3)∫_0 ^u (dx/(x−1)) −(1/6)∫_0 ^u ((2x+1+3)/(x^2 +x+1))dx =(1/3)[ln∣x−1∣]_0 ^u −(1/6)[ln(x^2 +x+1)]_0 ^u −(1/2)∫_0 ^u (dx/(x^2 +x+1)) =(1/3)ln∣u−1∣−(1/6)ln(u^2 +u+1)−(1/2)∫_0 ^u (dx/(x^2 +x+1)) but ∫_0 ^u (dx/(x^2 +x+1)) =∫_0 ^u (dx/((x+(1/2))^2 +(3/4))) =_(x+(1/2)=((√3)/2)z) (4/3) ∫_(1/( (√3))) ^((2u+1)/( (√3))) (1/(1+z^2 ))×((√3)/2)dz =(2/( (√3))) (arctan(((2u+1)/( (√3))))−arctan((1/( (√3))))) ⇒ ϕ(u) =−(2/( (√3))) arctan(((2u+1)/( (√3))))+(π/(3(√3))) ⇒ Σ_(n=0) ^∞ (t^n /(3n+1)) =(1/((^3 (√t))))ϕ(^3 (√t)) =(π/(3(√3)))−(2/( (√3))) arctan(((2(^3 (√t))+1)/( (√3)))) ⇒ Σ_(n=1) ^∞ (t^n /(3n+1)) =(π/(3(√3)))−1 −(2/( (√3))) arctan(((2(^3 (√t))+1)/( (√3)))) with t =(x/2)−1.

$$\left.\mathrm{4}\right)\:{let}\:{w}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left({x}−\mathrm{2}\right)^{{n}} }{\left(\mathrm{3}{n}+\mathrm{1}\right)\mathrm{2}^{{n}} }\:\Rightarrow{w}\left({x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{1}}\left(\frac{{x}−\mathrm{2}}{\mathrm{2}}\right)^{{n}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{3}{n}+\mathrm{1}}\left(\frac{{x}}{\mathrm{2}}−\mathrm{1}\right)^{{n}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{t}^{{n}} }{\mathrm{3}{n}+\mathrm{1}} \\ $$$${serie}\:{cv}\:\Rightarrow\mid\frac{{x}}{\mathrm{2}}−\mathrm{1}\mid<\mathrm{1}\:\Rightarrow\mid{x}−\mathrm{2}\mid<\mathrm{2}\:\Rightarrow−\mathrm{2}<{x}−\mathrm{2}<\mathrm{2}\:\Rightarrow\mathrm{0}<{x}<\mathrm{4} \\ $$$${in}\:{this}\:{case}\:\mid{t}\mid<\mathrm{1}\:\:\:{we}\:{have}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{t}^{{n}} }{\mathrm{3}{n}+\mathrm{1}}\:=\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{{t}}\right)}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(^{\mathrm{3}} \sqrt{{t}}\right)^{\mathrm{3}{n}+\mathrm{1}} }{\mathrm{3}{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{{t}}\right)}\varphi\left(^{\mathrm{3}} \sqrt{{t}}\right)\:\:\:{with}\:\varphi\left({u}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{\mathrm{3}{n}+\mathrm{1}} }{\mathrm{3}{n}+\mathrm{1}}\:\Rightarrow\varphi^{'} \left({u}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} {u}^{\mathrm{3}{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{u}^{\mathrm{3}} }\:\Rightarrow\:\varphi\left({u}\right)\:=\int_{\mathrm{0}} ^{{u}} \:\frac{{dx}}{\mathrm{1}−{x}^{\mathrm{3}} }\:+{c}\:\:\:\:\left({c}=\varphi\left(\mathrm{0}\right)\:=\mathrm{0}\right) \\ $$$$−\varphi\left({u}\right)\:=\int_{\mathrm{0}} ^{{u}} \:\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)}\:{let}\:{decompose} \\ $$$${F}\:=\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)}\:=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{{bx}\:+{c}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$${a}\:=\frac{\mathrm{1}}{\mathrm{3}}\:\:\:\:,\:\:{lim}_{{x}\rightarrow+\infty} {xF}\:\left({x}\right)=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}\:=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${F}\left(\mathrm{0}\right)\:=−\mathrm{1}\:=−{a}+{c}\:\Rightarrow{c}={a}−\mathrm{1}\:=−\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow \\ $$$${F}\:=\frac{\mathrm{1}}{\mathrm{3}\left({x}−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}}×\frac{{x}+\mathrm{2}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{{u}} \:{F}\left({x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{{u}} \:\frac{{dx}}{{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{{u}} \:\:\frac{\mathrm{2}{x}+\mathrm{1}+\mathrm{3}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[{ln}\mid{x}−\mathrm{1}\mid\right]_{\mathrm{0}} ^{{u}} \:−\frac{\mathrm{1}}{\mathrm{6}}\left[{ln}\left({x}^{\mathrm{2}} \:+{x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{{u}} −\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{u}} \:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{u}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{u}} \:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:\:{but} \\ $$$$\int_{\mathrm{0}} ^{{u}} \:\frac{{dx}}{{x}^{\mathrm{2}} \:+{x}+\mathrm{1}}\:=\int_{\mathrm{0}} ^{{u}} \:\frac{{dx}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{z}} \frac{\mathrm{4}}{\mathrm{3}}\:\:\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} }×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{dz} \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:\left({arctan}\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right)\:\Rightarrow \\ $$$$\varphi\left({u}\right)\:=−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{t}^{{n}} }{\mathrm{3}{n}+\mathrm{1}}\:=\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{{t}}\right)}\varphi\left(^{\mathrm{3}} \sqrt{{t}}\right)\:=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}\left(^{\mathrm{3}} \sqrt{{t}}\right)+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{\mathrm{3}{n}+\mathrm{1}}\:=\frac{\pi}{\mathrm{3}\sqrt{\mathrm{3}}}−\mathrm{1}\:−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}\left(^{\mathrm{3}} \sqrt{{t}}\right)+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$${with}\:{t}\:=\frac{{x}}{\mathrm{2}}−\mathrm{1}. \\ $$$$ \\ $$

Commented by Power last updated on 11/May/20

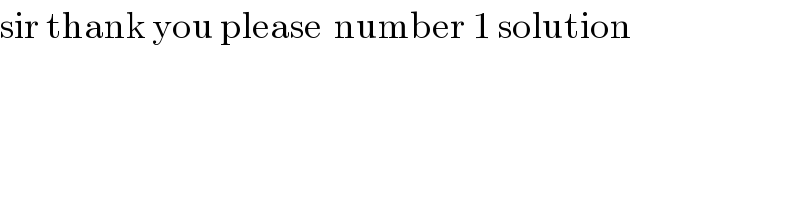
$$\mathrm{sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{please}\:\:\mathrm{number}\:\mathrm{1}\:\mathrm{solution} \\ $$

Commented by mathmax by abdo last updated on 11/May/20

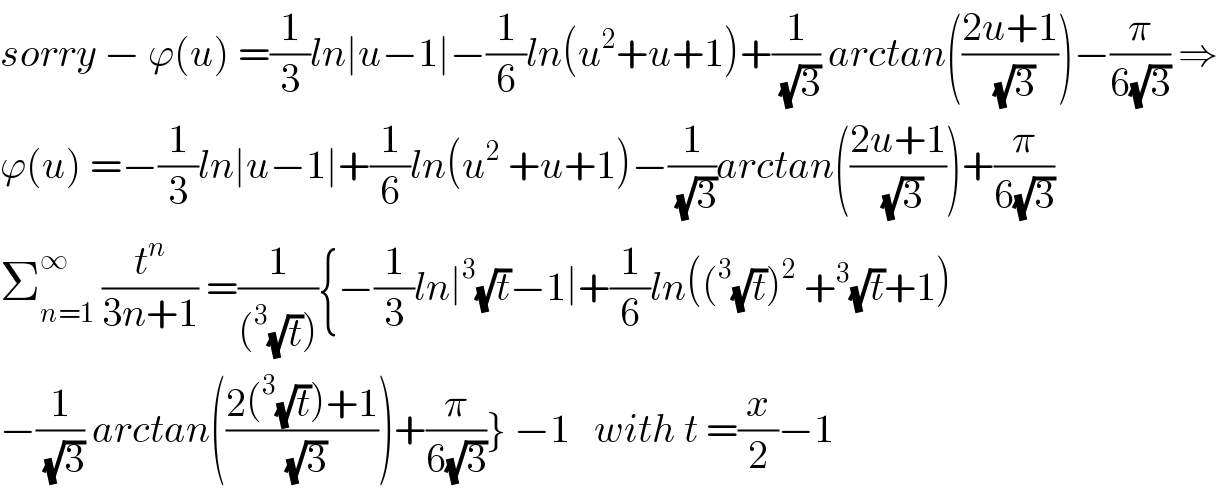
sorry − ϕ(u) =(1/3)ln∣u−1∣−(1/6)ln(u^2 +u+1)+(1/( (√3))) arctan(((2u+1)/( (√3))))−(π/(6(√3))) ⇒ ϕ(u) =−(1/3)ln∣u−1∣+(1/6)ln(u^2 +u+1)−(1/( (√3)))arctan(((2u+1)/( (√3))))+(π/(6(√3))) Σ_(n=1) ^∞ (t^n /(3n+1)) =(1/((^3 (√t)))){−(1/3)ln∣^3 (√t)−1∣+(1/6)ln((^3 (√t))^2 +^3 (√t)+1) −(1/( (√3))) arctan(((2(^3 (√t))+1)/( (√3))))+(π/(6(√3)))} −1 with t =(x/2)−1

$${sorry}\:−\:\varphi\left({u}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{u}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({u}^{\mathrm{2}} +{u}+\mathrm{1}\right)+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}\:\Rightarrow \\ $$$$\varphi\left({u}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid{u}−\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{6}}{ln}\left({u}^{\mathrm{2}} \:+{u}+\mathrm{1}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{2}{u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{t}^{{n}} }{\mathrm{3}{n}+\mathrm{1}}\:=\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{{t}}\right)}\left\{−\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid^{\mathrm{3}} \sqrt{{t}}−\mathrm{1}\mid+\frac{\mathrm{1}}{\mathrm{6}}{ln}\left(\left(^{\mathrm{3}} \sqrt{{t}}\right)^{\mathrm{2}} \:+^{\mathrm{3}} \sqrt{{t}}+\mathrm{1}\right)\right. \\ $$$$\left.−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:{arctan}\left(\frac{\mathrm{2}\left(^{\mathrm{3}} \sqrt{{t}}\right)+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}\right\}\:−\mathrm{1}\:\:\:{with}\:{t}\:=\frac{{x}}{\mathrm{2}}−\mathrm{1} \\ $$

Commented by mathmax by abdo last updated on 12/May/20

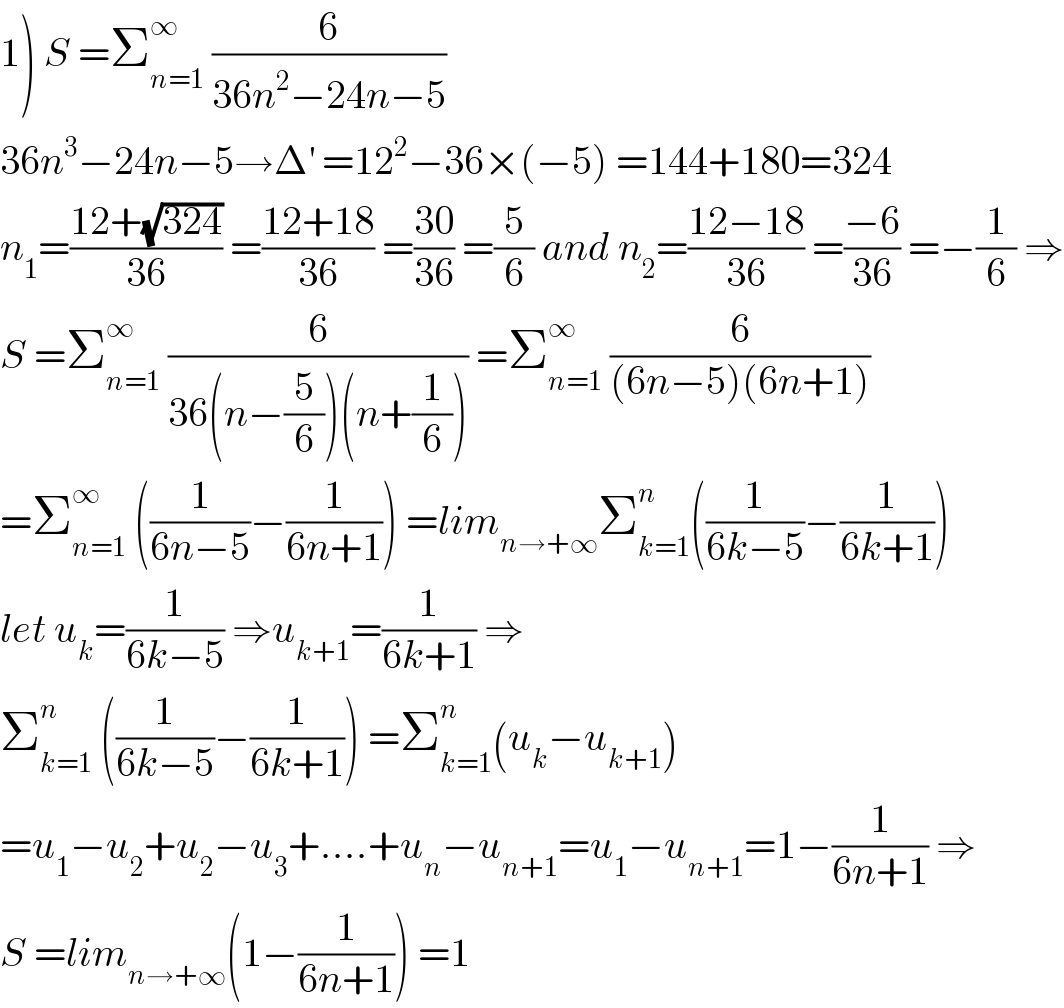
1) S =Σ_(n=1) ^∞ (6/(36n^2 −24n−5)) 36n^3 −24n−5→Δ^′ =12^2 −36×(−5) =144+180=324 n_1 =((12+(√(324)))/(36)) =((12+18)/(36)) =((30)/(36)) =(5/6) and n_2 =((12−18)/(36)) =((−6)/(36)) =−(1/6) ⇒ S =Σ_(n=1) ^∞ (6/(36(n−(5/6))(n+(1/6)))) =Σ_(n=1) ^∞ (6/((6n−5)(6n+1))) =Σ_(n=1) ^∞ ((1/(6n−5))−(1/(6n+1))) =lim_(n→+∞) Σ_(k=1) ^n ((1/(6k−5))−(1/(6k+1))) let u_k =(1/(6k−5)) ⇒u_(k+1) =(1/(6k+1)) ⇒ Σ_(k=1) ^n ((1/(6k−5))−(1/(6k+1))) =Σ_(k=1) ^n (u_k −u_(k+1) ) =u_1 −u_2 +u_2 −u_3 +....+u_n −u_(n+1) =u_1 −u_(n+1) =1−(1/(6n+1)) ⇒ S =lim_(n→+∞) (1−(1/(6n+1))) =1

$$\left.\mathrm{1}\right)\:{S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{6}}{\mathrm{36}{n}^{\mathrm{2}} −\mathrm{24}{n}−\mathrm{5}} \\ $$$$\mathrm{36}{n}^{\mathrm{3}} −\mathrm{24}{n}−\mathrm{5}\rightarrow\Delta^{'} \:=\mathrm{12}^{\mathrm{2}} −\mathrm{36}×\left(−\mathrm{5}\right)\:=\mathrm{144}+\mathrm{180}=\mathrm{324} \\ $$$${n}_{\mathrm{1}} =\frac{\mathrm{12}+\sqrt{\mathrm{324}}}{\mathrm{36}}\:=\frac{\mathrm{12}+\mathrm{18}}{\mathrm{36}}\:=\frac{\mathrm{30}}{\mathrm{36}}\:=\frac{\mathrm{5}}{\mathrm{6}}\:{and}\:{n}_{\mathrm{2}} =\frac{\mathrm{12}−\mathrm{18}}{\mathrm{36}}\:=\frac{−\mathrm{6}}{\mathrm{36}}\:=−\frac{\mathrm{1}}{\mathrm{6}}\:\Rightarrow \\ $$$${S}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{6}}{\mathrm{36}\left({n}−\frac{\mathrm{5}}{\mathrm{6}}\right)\left({n}+\frac{\mathrm{1}}{\mathrm{6}}\right)}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{6}}{\left(\mathrm{6}{n}−\mathrm{5}\right)\left(\mathrm{6}{n}+\mathrm{1}\right)} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(\frac{\mathrm{1}}{\mathrm{6}{n}−\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}{n}+\mathrm{1}}\right)\:={lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{1}} ^{{n}} \left(\frac{\mathrm{1}}{\mathrm{6}{k}−\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}{k}+\mathrm{1}}\right) \\ $$$${let}\:{u}_{{k}} =\frac{\mathrm{1}}{\mathrm{6}{k}−\mathrm{5}}\:\Rightarrow{u}_{{k}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{6}{k}+\mathrm{1}}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\left(\frac{\mathrm{1}}{\mathrm{6}{k}−\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}{k}+\mathrm{1}}\right)\:=\sum_{{k}=\mathrm{1}} ^{{n}} \left({u}_{{k}} −{u}_{{k}+\mathrm{1}} \right) \\ $$$$={u}_{\mathrm{1}} −{u}_{\mathrm{2}} +{u}_{\mathrm{2}} −{u}_{\mathrm{3}} +….+{u}_{{n}} −{u}_{{n}+\mathrm{1}} ={u}_{\mathrm{1}} −{u}_{{n}+\mathrm{1}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}{n}+\mathrm{1}}\:\Rightarrow \\ $$$${S}\:={lim}_{{n}\rightarrow+\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{6}{n}+\mathrm{1}}\right)\:=\mathrm{1} \\ $$

Commented by Power last updated on 12/May/20