Question Number 150626 by puissant last updated on 14/Aug/21
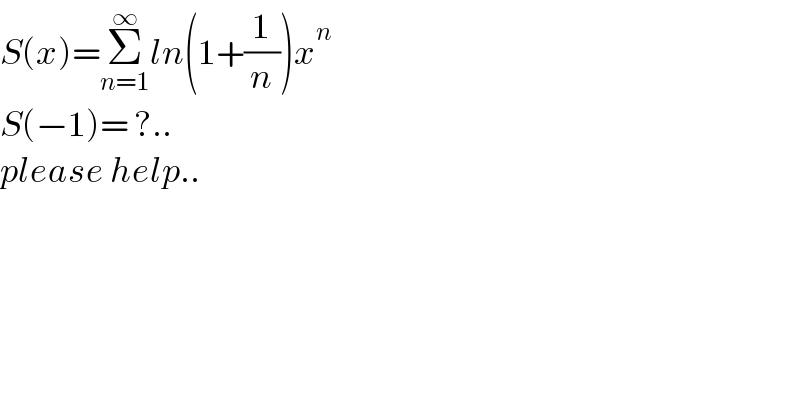
$${S}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right){x}^{{n}} \\ $$$${S}\left(−\mathrm{1}\right)=\:?.. \\ $$$${please}\:{help}.. \\ $$
Answered by puissant last updated on 14/Aug/21
![S(x)=Σ_(n=1) ^∞ ln(1+(1/n))x^n ; S(−1)=? S(−1)=Σ_(n=1) ^∞ (−1)^n (ln(n+1)−ln(n)) = lim_(p→∞) Σ_(n=1) ^(2p) (−1)^n (ln(n+1)−ln(n)) =lim_(p→∞) [2(−ln2+ln3+....−ln(2p))+ln(2p+1)] =lim_(p→∞) ln[(((3.5.7.....(2p−1))/(2.4.6.....2p)))^2 (2p+1)(((2.4...2p)/(2.4...2p)))^2 ] =lim_(p→∞) ln((((2p!)^2 (2p+1))/(2^(4p) (p!)^2 ))) D′apre^� s STIRLING, on a: (((2p!)^2 (2p+1))/(2^(2p) (p!)^4 )) ∼_(+∞) (((2p)/e))^4 ((((√(2pπ)))^4 (2p+1))/(2^(2p) ((p/e))^(4p) ((√(2pπ)))^4 )) ∼_(+∞) (2/π) ∵ ⇒ S(−1)=ln((2/π))...](https://www.tinkutara.com/question/Q150676.png)
$${S}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right){x}^{{n}} \:;\:{S}\left(−\mathrm{1}\right)=? \\ $$$${S}\left(−\mathrm{1}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left({ln}\left({n}+\mathrm{1}\right)−{ln}\left({n}\right)\right) \\ $$$$=\:{lim}_{{p}\rightarrow\infty} \underset{{n}=\mathrm{1}} {\overset{\mathrm{2}{p}} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left({ln}\left({n}+\mathrm{1}\right)−{ln}\left({n}\right)\right) \\ $$$$={lim}_{{p}\rightarrow\infty} \left[\mathrm{2}\left(−{ln}\mathrm{2}+{ln}\mathrm{3}+….−{ln}\left(\mathrm{2}{p}\right)\right)+{ln}\left(\mathrm{2}{p}+\mathrm{1}\right)\right] \\ $$$$={lim}_{{p}\rightarrow\infty} {ln}\left[\left(\frac{\mathrm{3}.\mathrm{5}.\mathrm{7}…..\left(\mathrm{2}{p}−\mathrm{1}\right)}{\mathrm{2}.\mathrm{4}.\mathrm{6}…..\mathrm{2}{p}}\right)^{\mathrm{2}} \left(\mathrm{2}{p}+\mathrm{1}\right)\left(\frac{\mathrm{2}.\mathrm{4}…\mathrm{2}{p}}{\mathrm{2}.\mathrm{4}…\mathrm{2}{p}}\right)^{\mathrm{2}} \right] \\ $$$$={lim}_{{p}\rightarrow\infty} {ln}\left(\frac{\left(\mathrm{2}{p}!\right)^{\mathrm{2}} \left(\mathrm{2}{p}+\mathrm{1}\right)}{\mathrm{2}^{\mathrm{4}{p}} \left({p}!\right)^{\mathrm{2}} }\right) \\ $$$${D}'{apr}\grave {{e}s}\:{STIRLING},\:{on}\:{a}: \\ $$$$\frac{\left(\mathrm{2}{p}!\right)^{\mathrm{2}} \left(\mathrm{2}{p}+\mathrm{1}\right)}{\mathrm{2}^{\mathrm{2}{p}} \left({p}!\right)^{\mathrm{4}} }\:\underset{+\infty} {\sim}\left(\frac{\mathrm{2}{p}}{{e}}\right)^{\mathrm{4}} \frac{\left(\sqrt{\mathrm{2}{p}\pi}\right)^{\mathrm{4}} \left(\mathrm{2}{p}+\mathrm{1}\right)}{\mathrm{2}^{\mathrm{2}{p}} \left(\frac{{p}}{{e}}\right)^{\mathrm{4}{p}} \left(\sqrt{\mathrm{2}{p}\pi}\right)^{\mathrm{4}} } \\ $$$$\underset{+\infty} {\sim}\frac{\mathrm{2}}{\pi} \\ $$$$\:\:\:\:\:\:\:\:\:\because\:\Rightarrow\:{S}\left(−\mathrm{1}\right)={ln}\left(\frac{\mathrm{2}}{\pi}\right)… \\ $$
Commented by Tawa11 last updated on 14/Aug/21

$$\mathrm{great} \\ $$
