Question Number 57572 by cesar.marval.larez@gmail.com last updated on 07/Apr/19
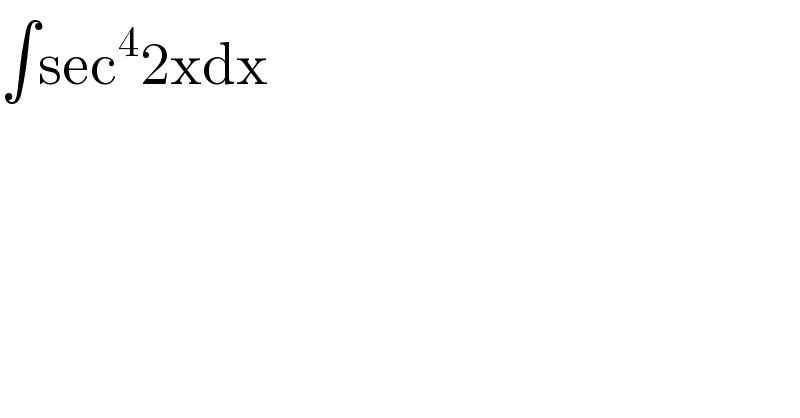
$$\int\mathrm{sec}^{\mathrm{4}} \mathrm{2xdx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Apr/19
![∫sec^2 2x×sec^2 2xdx ∫(1+tan^2 2x)sec^2 2xdx t=tan2x (dt/dx)=sec^2 2x×2 sec^2 2xdx=(dt/2) ∫(1+t^2 )×(dt/2) (1/2)[∫dt+∫t^2 dt] (1/2)(t+(t^3 /3))+c (1/2)(tan2x+((tan^3 2x)/3))+c](https://www.tinkutara.com/question/Q57573.png)
$$\int{sec}^{\mathrm{2}} \mathrm{2}{x}×{sec}^{\mathrm{2}} \mathrm{2}{xdx} \\ $$$$\int\left(\mathrm{1}+{tan}^{\mathrm{2}} \mathrm{2}{x}\right){sec}^{\mathrm{2}} \mathrm{2}{xdx} \\ $$$${t}={tan}\mathrm{2}{x} \\ $$$$\frac{{dt}}{{dx}}={sec}^{\mathrm{2}} \mathrm{2}{x}×\mathrm{2} \\ $$$${sec}^{\mathrm{2}} \mathrm{2}{xdx}=\frac{{dt}}{\mathrm{2}} \\ $$$$\int\left(\mathrm{1}+{t}^{\mathrm{2}} \right)×\frac{{dt}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\int{dt}+\int{t}^{\mathrm{2}} {dt}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({t}+\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\right)+{c} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({tan}\mathrm{2}{x}+\frac{{tan}^{\mathrm{3}} \mathrm{2}{x}}{\mathrm{3}}\right)+{c} \\ $$$$ \\ $$$$ \\ $$
