Question Number 92119 by M±th+et+s last updated on 04/May/20
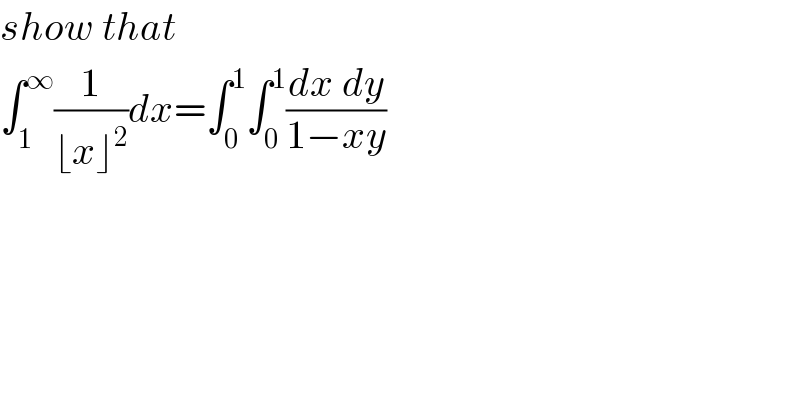
$${show}\:{that}\: \\ $$$$\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\lfloor{x}\rfloor^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}\:{dy}}{\mathrm{1}−{xy}} \\ $$
Commented by mathmax by abdo last updated on 05/May/20
![∫_0 ^1 (dx/(1−xy)) =−(1/y)[ln∣1−xy∣]_0 ^1 =−(1/y){ln(1−y)} ⇒ ∫_0 ^1 ∫_0 ^1 (1/(1−xy))dxdy =−∫_0 ^1 ((ln(1−y))/y)dy we have ln^′ (1−y) =−(1/(1−y)) =−Σ_(n=0) ^∞ y^n ⇒ ln(1−y) =−Σ_(n=0) ^∞ (y^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (y^n /n) ⇒−((ln(1−y))/y) =Σ_(n=1) ^∞ (y^(n−1) /n) ⇒−∫_0 ^1 ((ln(1−y))/y)dy =Σ_(n=1) ^∞ (1/n)∫_0 ^1 y^(n−1) dy =Σ_(n=1) ^∞ (1/n^2 ) also we have ∫_1 ^(+∞) (dx/([x]^2 )) =Σ_(n=1) ^∞ ∫_n ^(n+1) (dx/n^2 ) =Σ_(n=1) ^∞ (1/n^2 ) ⇒ ∫_0 ^1 ∫_0 ^1 (1/(1−xy))dxdy =∫_1 ^∞ (dx/([x]^2 )) (=(π^2 /6))](https://www.tinkutara.com/question/Q92128.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}−{xy}}\:=−\frac{\mathrm{1}}{{y}}\left[{ln}\mid\mathrm{1}−{xy}\mid\right]_{\mathrm{0}} ^{\mathrm{1}} \:=−\frac{\mathrm{1}}{{y}}\left\{{ln}\left(\mathrm{1}−{y}\right)\right\}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}−{xy}}{dxdy}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{y}\right)}{{y}}{dy} \\ $$$${we}\:{have}\:{ln}^{'} \left(\mathrm{1}−{y}\right)\:=−\frac{\mathrm{1}}{\mathrm{1}−{y}}\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{y}^{{n}} \:\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{y}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{y}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=−\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{y}^{{n}} }{{n}}\:\Rightarrow−\frac{{ln}\left(\mathrm{1}−{y}\right)}{{y}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{{y}^{{n}−\mathrm{1}} }{{n}} \\ $$$$\Rightarrow−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left(\mathrm{1}−{y}\right)}{{y}}{dy}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:{y}^{{n}−\mathrm{1}} {dy} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\:{also}\:{we}\:{have} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{{dx}}{\left[{x}\right]^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\int_{{n}} ^{{n}+\mathrm{1}} \:\frac{{dx}}{{n}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}−{xy}}{dxdy}\:=\int_{\mathrm{1}} ^{\infty} \:\frac{{dx}}{\left[{x}\right]^{\mathrm{2}} }\:\:\left(=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\right) \\ $$
Commented by M±th+et+s last updated on 05/May/20
$${very}\:{cool}\:{thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 05/May/20
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
