Question Number 98060 by M±th+et+s last updated on 11/Jun/20
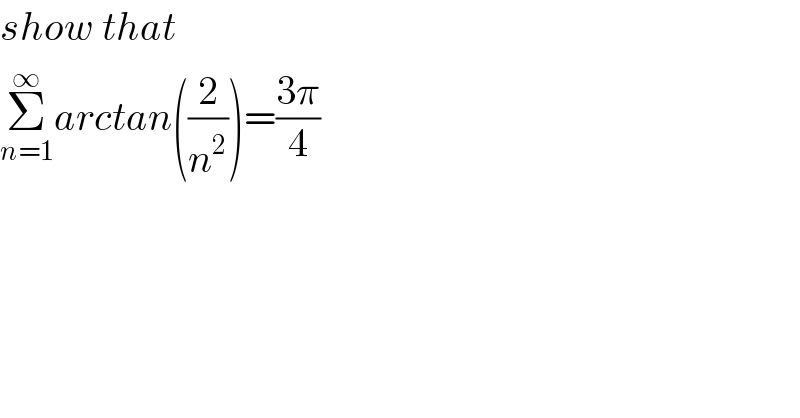
$${show}\:{that} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{arctan}\left(\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\right)=\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$
Answered by smridha last updated on 11/Jun/20

$${is}\:{it}\:\boldsymbol{{right}}\:\boldsymbol{{ans}}???\boldsymbol{{I}}\:{think}\:\boldsymbol{{it}}'{s}\:{just} \\ $$$$\frac{\boldsymbol{\pi}}{\mathrm{4}}…\boldsymbol{{and}}\:\boldsymbol{{also}}\:\boldsymbol{{I}}\:\boldsymbol{{prove}}\:\boldsymbol{{this}}.. \\ $$
Commented by M±th+et+s last updated on 11/Jun/20

Commented by smridha last updated on 11/Jun/20
![Σ_(n=1) ^∞ tan^(−1) [(((n+1)−(n−1))/(1+(n+1)(n−1)))] =Σ_(n=0) ^∞ [tan^(−1) (n+1)−tan^(−1) (n−1)] now partial sum of sequence.. S_1 =tan^(−1) (2)−tan^(−1) (0) S_2 =tan^(−1) (2)+tan^(−1) (3)−tan^(−1) (1) S_3 =tan^(−1) (3)+tan^(−1) (4)−tan^(−1) (1) .................. .................. S_n =tan^(−1) (n+1)+tan^(−1) (n−1)−(𝛑/4) now , lim_(n→∞) S_n =(𝛑/2)+(𝛑/2)−(𝛑/4)=((3π)/4) sorry for miss judgement at first it′s perfect.. okk thanks](https://www.tinkutara.com/question/Q98072.png)
$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{\left({n}+\mathrm{1}\right)−\left({n}−\mathrm{1}\right)}{\mathrm{1}+\left(\boldsymbol{{n}}+\mathrm{1}\right)\left(\boldsymbol{{n}}−\mathrm{1}\right)}\right] \\ $$$$=\underset{\boldsymbol{{n}}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\boldsymbol{{n}}+\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\boldsymbol{{n}}−\mathrm{1}\right)\right] \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{partial}}\:\boldsymbol{{sum}}\:\boldsymbol{{of}}\:\boldsymbol{{sequence}}.. \\ $$$$\boldsymbol{{S}}_{\mathrm{1}} =\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{0}\right) \\ $$$$\boldsymbol{{S}}_{\mathrm{2}} =\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right) \\ $$$$\boldsymbol{{S}}_{\mathrm{3}} =\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{4}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right) \\ $$$$……………… \\ $$$$……………… \\ $$$$\boldsymbol{{S}}_{\boldsymbol{{n}}} =\mathrm{tan}^{−\mathrm{1}} \left(\boldsymbol{{n}}+\mathrm{1}\right)+\mathrm{tan}^{−\mathrm{1}} \left(\boldsymbol{{n}}−\mathrm{1}\right)−\frac{\boldsymbol{\pi}}{\mathrm{4}} \\ $$$$\boldsymbol{{now}}\:, \\ $$$$\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\boldsymbol{{S}}_{\boldsymbol{{n}}} =\frac{\boldsymbol{\pi}}{\mathrm{2}}+\frac{\boldsymbol{\pi}}{\mathrm{2}}−\frac{\boldsymbol{\pi}}{\mathrm{4}}=\frac{\mathrm{3}\pi}{\mathrm{4}} \\ $$$$\boldsymbol{{sorry}}\:\boldsymbol{{for}}\:\boldsymbol{{miss}}\:\boldsymbol{{judgement}}\:\boldsymbol{{at}}\:\boldsymbol{{first}} \\ $$$$\boldsymbol{{it}}'{s}\:\boldsymbol{{perfect}}.. \\ $$$$\boldsymbol{{okk}}\:\boldsymbol{{thanks}} \\ $$
Commented by M±th+et+s last updated on 11/Jun/20

$${intellignt}. \\ $$$${thank}\:{you}\:{sir} \\ $$
