Question Number 95592 by i jagooll last updated on 26/May/20
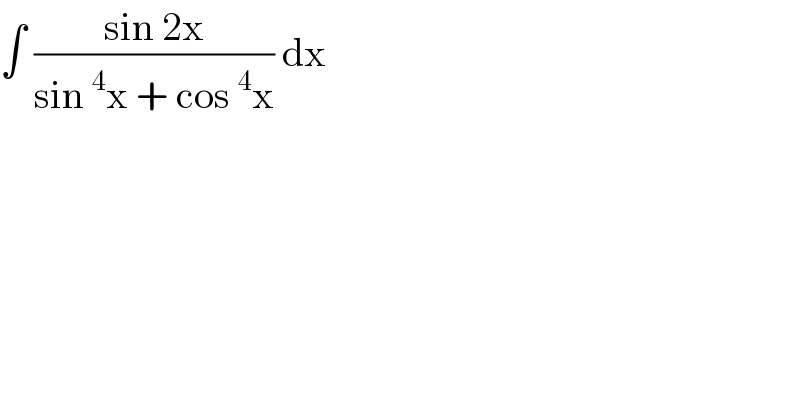
$$\int\:\frac{\mathrm{sin}\:\mathrm{2x}}{\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}\:+\:\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}}\:\mathrm{dx} \\ $$
Commented by PRITHWISH SEN 2 last updated on 26/May/20
![∫((2sin 2x dx)/(2−sin^2 2x)) = ∫[(1/( (√2)−sin 2x)) − (1/( (√2)+sin 2x)) ] dx](https://www.tinkutara.com/question/Q95595.png)
$$\int\frac{\mathrm{2sin}\:\mathrm{2x}\:\mathrm{dx}}{\mathrm{2}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x}}\:=\:\int\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{sin}\:\mathrm{2x}}\:−\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{sin}\:\mathrm{2x}}\:\right]\:\mathrm{dx} \\ $$
