Question Number 106807 by Study last updated on 07/Aug/20
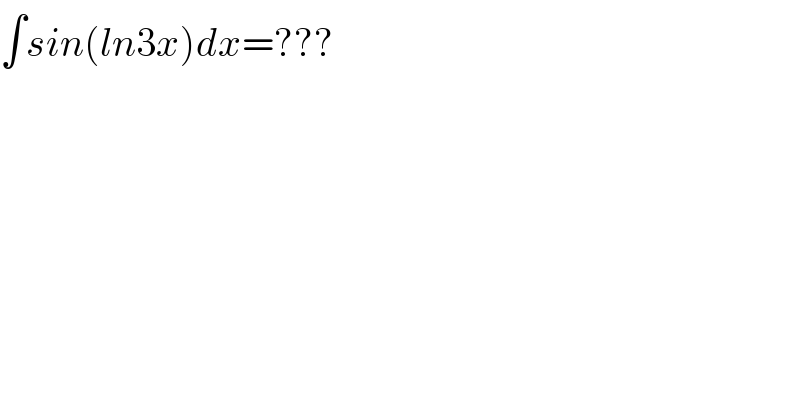
$$\int{sin}\left({ln}\mathrm{3}{x}\right){dx}=??? \\ $$
Answered by bemath last updated on 08/Aug/20
![@bemath@ ln 3x=u ⇒3x=e^u ; dx = ((e^u du)/3) J=∫ sin (u)((e^u /3) du) J=(1/3)∫ e^u sin u du [ by parts ] J=(1/3)[−e^u cos u+∫ e^u cos u du ] J=−(1/3)e^u cos u+(1/3)[e^u sin u−∫e^u sin u du ] J+(1/3)J=−(1/3)e^u (cos u−sin u) J=(3/4)×(−(1/3)e^u (cos u−sin u))+C J=−((3x)/4) (cos (ln 3x)−sin (ln 3x))+C](https://www.tinkutara.com/question/Q106946.png)
$$\:\:\:\:\:\:\:\:@\mathrm{bemath}@ \\ $$$$\mathrm{ln}\:\mathrm{3x}=\mathrm{u}\:\Rightarrow\mathrm{3x}=\mathrm{e}^{\mathrm{u}} \:;\:\mathrm{dx}\:=\:\frac{\mathrm{e}^{\mathrm{u}} \:\mathrm{du}}{\mathrm{3}} \\ $$$$\mathrm{J}=\int\:\mathrm{sin}\:\left(\mathrm{u}\right)\left(\frac{\mathrm{e}^{\mathrm{u}} }{\mathrm{3}}\:\mathrm{du}\right) \\ $$$$\mathrm{J}=\frac{\mathrm{1}}{\mathrm{3}}\int\:\mathrm{e}^{\mathrm{u}} \:\mathrm{sin}\:\mathrm{u}\:\mathrm{du}\:\:\:\left[\:\mathrm{by}\:\mathrm{parts}\:\right] \\ $$$$\mathrm{J}=\frac{\mathrm{1}}{\mathrm{3}}\left[−\mathrm{e}^{\mathrm{u}} \:\mathrm{cos}\:\mathrm{u}+\int\:\mathrm{e}^{\mathrm{u}} \:\mathrm{cos}\:\mathrm{u}\:\mathrm{du}\:\right] \\ $$$$\mathrm{J}=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{u}} \:\mathrm{cos}\:\mathrm{u}+\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{e}^{\mathrm{u}} \:\mathrm{sin}\:\mathrm{u}−\int\mathrm{e}^{\mathrm{u}} \:\mathrm{sin}\:\mathrm{u}\:\mathrm{du}\:\right] \\ $$$$\mathrm{J}+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{J}=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{u}} \:\left(\mathrm{cos}\:\mathrm{u}−\mathrm{sin}\:\mathrm{u}\right) \\ $$$$\mathrm{J}=\frac{\mathrm{3}}{\mathrm{4}}×\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{e}^{\mathrm{u}} \:\left(\mathrm{cos}\:\mathrm{u}−\mathrm{sin}\:\mathrm{u}\right)\right)+\mathrm{C} \\ $$$$\mathrm{J}=−\frac{\mathrm{3x}}{\mathrm{4}}\:\left(\mathrm{cos}\:\left(\mathrm{ln}\:\mathrm{3x}\right)−\mathrm{sin}\:\left(\mathrm{ln}\:\mathrm{3x}\right)\right)+\mathrm{C} \\ $$
