Question Number 88045 by jagoll last updated on 08/Apr/20
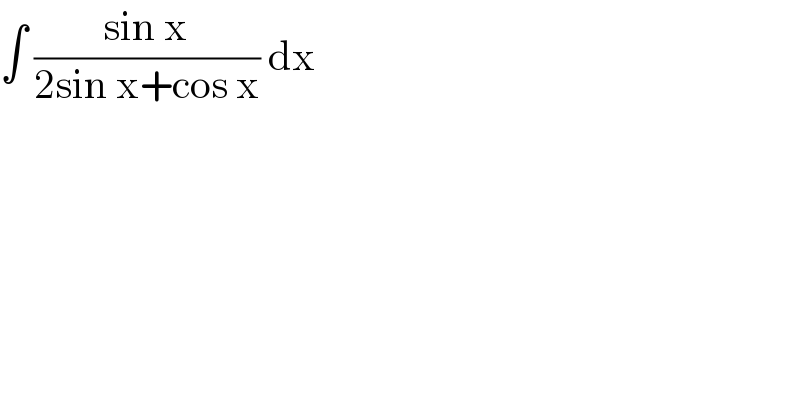
$$\int\:\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{2sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:\mathrm{dx}\: \\ $$
Commented by john santu last updated on 08/Apr/20
![((sin x)/(2sin x+cos x)) = (2/5)−(1/5)[((2cos x−sin x)/(2sin x+cos x)) ] ⇒ ∫ {(2/5)−(1/5)[((2cos x−sin x)/(2sin x+cos x)) ]} dx = ((2x)/5)− (1/5) log ∣ 2sin x+cos x ∣ + c](https://www.tinkutara.com/question/Q88046.png)
$$\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{2sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:=\:\frac{\mathrm{2}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{5}}\left[\frac{\mathrm{2cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{2sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:\right] \\ $$$$\Rightarrow\:\int\:\left\{\frac{\mathrm{2}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{5}}\left[\frac{\mathrm{2cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{2sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}\:\right]\right\}\:\mathrm{dx} \\ $$$$=\:\frac{\mathrm{2x}}{\mathrm{5}}−\:\frac{\mathrm{1}}{\mathrm{5}}\:\mathrm{log}\:\mid\:\mathrm{2sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\:\mid\:+\:\mathrm{c} \\ $$
Commented by jagoll last updated on 08/Apr/20
$$\mathrm{waw}…\mathrm{super}\:\mathrm{easy}\: \\ $$
