Question Number 131021 by mohammad17 last updated on 31/Jan/21

$${solve} \\ $$$$ \\ $$$$\left(\mathrm{1}\right):\left(\mathrm{1}+{i}\right)^{{i}} \\ $$$$ \\ $$$$\left(\mathrm{2}\right):\:{log}\left(\mathrm{1}+{i}\right)^{\pi{i}} \\ $$
Answered by Dwaipayan Shikari last updated on 31/Jan/21
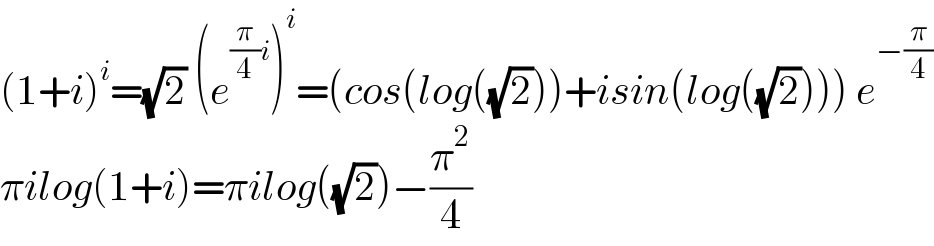
$$\left(\mathrm{1}+{i}\right)^{{i}} =\sqrt{\mathrm{2}}\:\left({e}^{\frac{\pi}{\mathrm{4}}{i}} \right)^{{i}} =\left({cos}\left({log}\left(\sqrt{\mathrm{2}}\right)\right)+{isin}\left({log}\left(\sqrt{\mathrm{2}}\right)\right)\right)\:{e}^{−\frac{\pi}{\mathrm{4}}} \\ $$$$\pi{ilog}\left(\mathrm{1}+{i}\right)=\pi{ilog}\left(\sqrt{\mathrm{2}}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$
Answered by mr W last updated on 31/Jan/21
![(1) (1+i)=(√2)e^((πi)/4) =e^(ln (√2)+((πi)/4)) (1+i)^i =e^((ln (√2)+((πi)/4))i) =e^(−(π/4)) e^(i ln (√2)) =e^(−(π/4)) [cos (ln (√2))+i sin (ln (√2))] (2) ln (1+i)^(πi) =πi ln [e^(ln (√2)+((πi)/4)) ] =πi(ln (√2)+((πi)/4)) =π(−(π/4)+i ln (√2))](https://www.tinkutara.com/question/Q131032.png)
$$\left(\mathrm{1}\right) \\ $$$$\left(\mathrm{1}+{i}\right)=\sqrt{\mathrm{2}}{e}^{\frac{\pi{i}}{\mathrm{4}}} ={e}^{\mathrm{ln}\:\sqrt{\mathrm{2}}+\frac{\pi{i}}{\mathrm{4}}} \\ $$$$\left(\mathrm{1}+{i}\right)^{{i}} ={e}^{\left(\mathrm{ln}\:\sqrt{\mathrm{2}}+\frac{\pi{i}}{\mathrm{4}}\right){i}} ={e}^{−\frac{\pi}{\mathrm{4}}} {e}^{{i}\:\mathrm{ln}\:\sqrt{\mathrm{2}}} \\ $$$$={e}^{−\frac{\pi}{\mathrm{4}}} \left[\mathrm{cos}\:\left(\mathrm{ln}\:\sqrt{\mathrm{2}}\right)+{i}\:\mathrm{sin}\:\left(\mathrm{ln}\:\sqrt{\mathrm{2}}\right)\right] \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$\mathrm{ln}\:\left(\mathrm{1}+{i}\right)^{\pi{i}} =\pi{i}\:\mathrm{ln}\:\left[{e}^{\mathrm{ln}\:\sqrt{\mathrm{2}}+\frac{\pi{i}}{\mathrm{4}}} \right] \\ $$$$=\pi{i}\left(\mathrm{ln}\:\sqrt{\mathrm{2}}+\frac{\pi{i}}{\mathrm{4}}\right) \\ $$$$=\pi\left(−\frac{\pi}{\mathrm{4}}+{i}\:\mathrm{ln}\:\sqrt{\mathrm{2}}\right) \\ $$
