Question Number 115026 by jm2bok last updated on 23/Sep/20
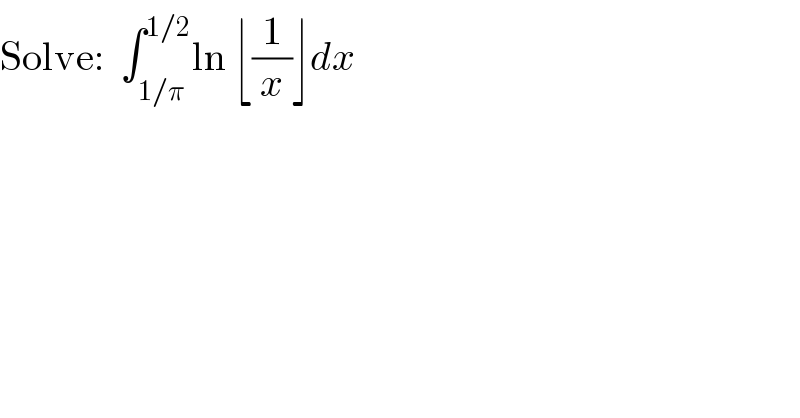
$$\mathrm{Solve}:\:\:\int_{\mathrm{1}/\pi} ^{\mathrm{1}/\mathrm{2}} \mathrm{ln}\:\lfloor\frac{\mathrm{1}}{{x}}\rfloor{dx} \\ $$
Answered by PRITHWISH SEN 2 last updated on 23/Sep/20

$$\mathrm{when} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\pi}\leqslant\mathrm{x}\leqslant\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:\mathrm{3}\leqslant\frac{\mathrm{1}}{\mathrm{x}}\leqslant\pi\:\Rightarrow\mathrm{ln}\lfloor\frac{\mathrm{1}}{\mathrm{x}}\rfloor=\mathrm{ln3} \\ $$$$\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{3}}<\mathrm{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\:\mathrm{2}\leqslant\mathrm{x}<\mathrm{3}\Rightarrow\mathrm{ln}\lfloor\frac{\mathrm{1}}{\mathrm{x}}\rfloor=\mathrm{ln2} \\ $$$$\therefore\:\mathrm{the}\:\mathrm{integration} \\ $$$$\:\:=\:\int_{\frac{\mathrm{1}}{\pi}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{ln}\left(\mathrm{3}\right)\mathrm{dx}\:+\int_{\frac{\mathrm{1}}{\mathrm{3}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{ln}\left(\mathrm{2}\right)\mathrm{dx} \\ $$$$=\:\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\pi}\right)\mathrm{ln3}+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)\mathrm{ln2}\:\backsim\:\mathrm{0}.\mathrm{13202947375} \\ $$
Answered by mathmax by abdo last updated on 23/Sep/20
![I =∫_(1/π) ^(1/2) ln{[(1/x)]}dx we do the changement (1/x)=t ⇒ I =∫_π ^2 ln{[t]}(−(dt/t^2 )) =∫_2 ^π ((ln[t])/t^2 ) dt (π∼3,14) ⇒ I =∫_2 ^3 ((ln[t])/t^2 )dt +∫_3 ^π ((ln[t])/t^2 )dt =2 ∫_2 ^3 (dt/t^2 ) +3 ∫_3 ^π (dt/t^2 ) =2[−(1/t)]_2 ^3 +3[−(1/t)]_3 ^π =2((1/2)−(1/3)) +3((1/3)−(1/π)) =1−(2/3) +1−(3/π) =2−(2/3)−(3/π) =(4/3)−(3/π)](https://www.tinkutara.com/question/Q115089.png)
$$\mathrm{I}\:=\int_{\frac{\mathrm{1}}{\pi}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{ln}\left\{\left[\frac{\mathrm{1}}{\mathrm{x}}\right]\right\}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\pi} ^{\mathrm{2}} \:\mathrm{ln}\left\{\left[\mathrm{t}\right]\right\}\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right)\:=\int_{\mathrm{2}} ^{\pi} \:\frac{\mathrm{ln}\left[\mathrm{t}\right]}{\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt}\:\:\:\:\:\:\:\:\:\left(\pi\sim\mathrm{3},\mathrm{14}\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{2}} ^{\mathrm{3}} \frac{\mathrm{ln}\left[\mathrm{t}\right]}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:+\int_{\mathrm{3}} ^{\pi} \:\frac{\mathrm{ln}\left[\mathrm{t}\right]}{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\mathrm{2}\:\int_{\mathrm{2}} ^{\mathrm{3}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\:+\mathrm{3}\:\int_{\mathrm{3}} ^{\pi} \:\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\left[−\frac{\mathrm{1}}{\mathrm{t}}\right]_{\mathrm{2}} ^{\mathrm{3}} \:+\mathrm{3}\left[−\frac{\mathrm{1}}{\mathrm{t}}\right]_{\mathrm{3}} ^{\pi} \:=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)\:+\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\pi}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}\:+\mathrm{1}−\frac{\mathrm{3}}{\pi}\:=\mathrm{2}−\frac{\mathrm{2}}{\mathrm{3}}−\frac{\mathrm{3}}{\pi}\:=\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{3}}{\pi} \\ $$
