Question Number 116303 by Engr_Jidda last updated on 02/Oct/20
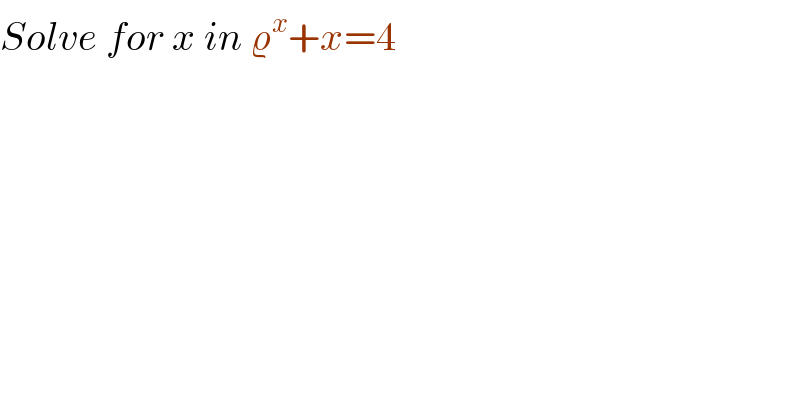
$${Solve}\:{for}\:{x}\:{in}\:\varrho^{{x}} +{x}=\mathrm{4} \\ $$
Answered by mr W last updated on 02/Oct/20
![ϱ^x =4−x ϱ^4 =ϱ^(4−x) (4−x) ϱ^4 =(4−x)e^((4−x)ln ϱ) ϱ^4 ln ϱ=[(4−x)ln ϱ] e^((4−x)ln ϱ) ⇒(4−x)ln ϱ=W(ϱ^4 ln ϱ) ⇒x=4−((W(ϱ^4 ln ϱ))/(ln ϱ))](https://www.tinkutara.com/question/Q116307.png)
$$\varrho^{{x}} =\mathrm{4}−{x} \\ $$$$\varrho^{\mathrm{4}} =\varrho^{\mathrm{4}−{x}} \left(\mathrm{4}−{x}\right) \\ $$$$\varrho^{\mathrm{4}} =\left(\mathrm{4}−{x}\right){e}^{\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\varrho} \\ $$$$\varrho^{\mathrm{4}} \mathrm{ln}\:\varrho=\left[\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\varrho\right]\:{e}^{\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\varrho} \\ $$$$\Rightarrow\left(\mathrm{4}−{x}\right)\mathrm{ln}\:\varrho=\mathbb{W}\left(\varrho^{\mathrm{4}} \mathrm{ln}\:\varrho\right) \\ $$$$\Rightarrow{x}=\mathrm{4}−\frac{\mathbb{W}\left(\varrho^{\mathrm{4}} \mathrm{ln}\:\varrho\right)}{\mathrm{ln}\:\varrho} \\ $$
Commented by Engr_Jidda last updated on 02/Oct/20

$${thank}\:{you}\:{sir} \\ $$
