Question Number 160987 by cortano last updated on 10/Dec/21
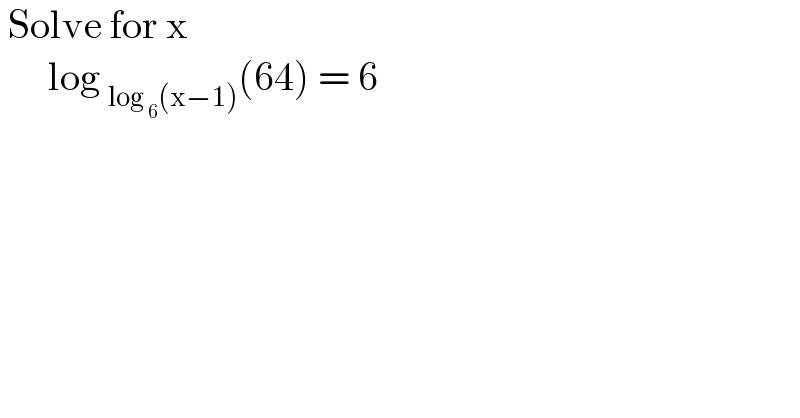
$$\:\mathrm{Solve}\:\mathrm{for}\:\mathrm{x}\: \\ $$$$\:\:\:\:\:\:\mathrm{log}\:_{\mathrm{log}\:_{\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right)} \left(\mathrm{64}\right)\:=\:\mathrm{6}\: \\ $$
Answered by bobhans last updated on 10/Dec/21
![log _(log _6 (x−1)) (64) = 6 [ log _6 (x−1)]^6 = 64 log _6 (x−1)= ± 2 (x−1)= { (6^(−2) ),(6^2 ) :}⇒ { ((x=1+(1/(36))=((37)/(36)))),((x=1+36=37)) :}](https://www.tinkutara.com/question/Q160990.png)
$$\:\:\mathrm{log}\:_{\mathrm{log}\:_{\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right)} \left(\mathrm{64}\right)\:=\:\mathrm{6}\: \\ $$$$\:\:\left[\:\mathrm{log}\:_{\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right)\right]^{\mathrm{6}} \:=\:\mathrm{64} \\ $$$$\:\:\mathrm{log}\:_{\mathrm{6}} \left(\mathrm{x}−\mathrm{1}\right)=\:\pm\:\mathrm{2}\: \\ $$$$\:\:\left(\mathrm{x}−\mathrm{1}\right)=\begin{cases}{\mathrm{6}^{−\mathrm{2}} }\\{\mathrm{6}^{\mathrm{2}} }\end{cases}\Rightarrow\begin{cases}{\mathrm{x}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{36}}=\frac{\mathrm{37}}{\mathrm{36}}}\\{\mathrm{x}=\mathrm{1}+\mathrm{36}=\mathrm{37}}\end{cases} \\ $$
