Question Number 110246 by Her_Majesty last updated on 28/Aug/20
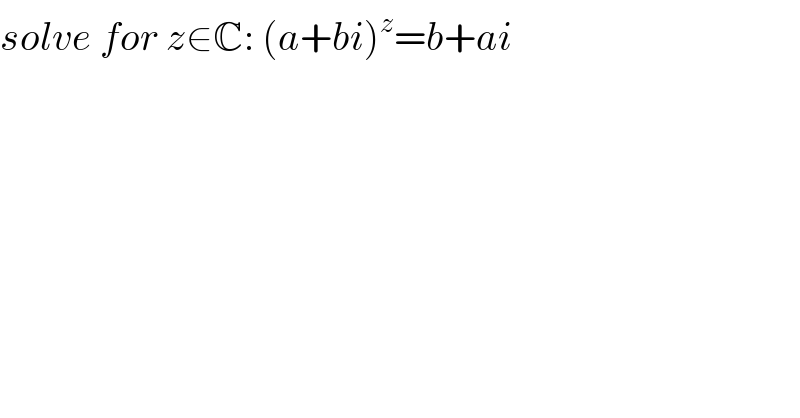
$${solve}\:{for}\:{z}\in\mathbb{C}:\:\left({a}+{bi}\right)^{{z}} ={b}+{ai} \\ $$
Answered by mr W last updated on 28/Aug/20
![θ=tan^(−1) (b/a) zln (a+bi)=ln (b+ai) z(ln (√(a^2 +b^2 ))+iθ)=ln (√(a^2 +b^2 ))+i((π/2)−θ) z=((ln (√(a^2 +b^2 ))+i((π/2)−θ))/(ln (√(a^2 +b^2 ))+iθ)) z=(([ln (√(a^2 +b^2 ))+i((π/2)−θ)][ln (√(a^2 +b^2 ))+iθ])/(ln^2 (√(a^2 +b^2 ))+θ^2 )) z=((ln^2 (√(a^2 +b^2 ))+((π/2)−θ)θ+(π/2)ln (√(a^2 +b^2 ))i)/(ln^2 (√(a^2 +b^2 ))+θ^2 ))](https://www.tinkutara.com/question/Q110270.png)
$$\theta=\mathrm{tan}^{−\mathrm{1}} \frac{{b}}{{a}} \\ $$$${z}\mathrm{ln}\:\left({a}+{bi}\right)=\mathrm{ln}\:\left({b}+{ai}\right) \\ $$$${z}\left(\mathrm{ln}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{i}\theta\right)=\mathrm{ln}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{i}\left(\frac{\pi}{\mathrm{2}}−\theta\right) \\ $$$${z}=\frac{\mathrm{ln}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{i}\left(\frac{\pi}{\mathrm{2}}−\theta\right)}{\mathrm{ln}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{i}\theta} \\ $$$${z}=\frac{\left[\mathrm{ln}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{i}\left(\frac{\pi}{\mathrm{2}}−\theta\right)\right]\left[\mathrm{ln}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{i}\theta\right]}{\mathrm{ln}^{\mathrm{2}} \:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\theta^{\mathrm{2}} } \\ $$$${z}=\frac{\mathrm{ln}^{\mathrm{2}} \:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\left(\frac{\pi}{\mathrm{2}}−\theta\right)\theta+\frac{\pi}{\mathrm{2}}\mathrm{ln}\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{i}}{\mathrm{ln}^{\mathrm{2}} \:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+\theta^{\mathrm{2}} } \\ $$
Commented by Her_Majesty last updated on 28/Aug/20

$${thank}\:{you} \\ $$
