Question Number 101553 by bobhans last updated on 03/Jul/20
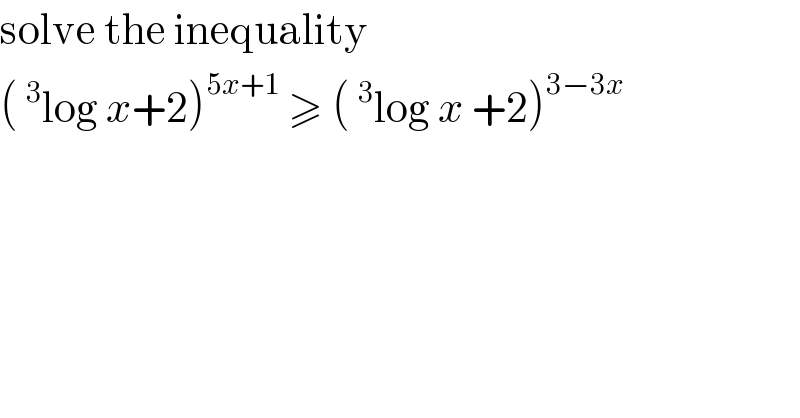
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{inequality} \\ $$$$\left(\:^{\mathrm{3}} \mathrm{log}\:{x}+\mathrm{2}\right)^{\mathrm{5}{x}+\mathrm{1}} \:\geqslant\:\left(\:^{\mathrm{3}} \mathrm{log}\:{x}\:+\mathrm{2}\right)^{\mathrm{3}−\mathrm{3}{x}} \\ $$
Answered by bramlex last updated on 03/Jul/20
![→(log _3 x+2−1)(5x+1−3+3x)≥0 (log _3 x +1)(8x−2)≥0 case(1) log _3 x+1≥0 ∧8x−2≥0 x ≥(1/3) ∧ x≥(1/4) ⇔x≥(1/3) case(2) log _3 x +1≤0 ∧ 8x−2≤0 x ≤(1/3) ∧x≤(1/4) ∧x > 0⇒0< x ≤(1/4) we get solution is x∈ (0, (1/4)] ∪ [ (1/3),∞) ★](https://www.tinkutara.com/question/Q101562.png)
$$\rightarrow\left(\mathrm{log}\:_{\mathrm{3}} \:{x}+\mathrm{2}−\mathrm{1}\right)\left(\mathrm{5}{x}+\mathrm{1}−\mathrm{3}+\mathrm{3}{x}\right)\geqslant\mathrm{0} \\ $$$$\left(\mathrm{log}\:_{\mathrm{3}} {x}\:+\mathrm{1}\right)\left(\mathrm{8}{x}−\mathrm{2}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{log}\:_{\mathrm{3}} {x}+\mathrm{1}\geqslant\mathrm{0}\:\wedge\mathrm{8}{x}−\mathrm{2}\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}\:\geqslant\frac{\mathrm{1}}{\mathrm{3}}\:\wedge\:{x}\geqslant\frac{\mathrm{1}}{\mathrm{4}}\:\Leftrightarrow{x}\geqslant\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{log}\:_{\mathrm{3}} {x}\:+\mathrm{1}\leqslant\mathrm{0}\:\wedge\:\mathrm{8}{x}−\mathrm{2}\leqslant\mathrm{0} \\ $$$$\:{x}\:\leqslant\frac{\mathrm{1}}{\mathrm{3}}\:\wedge{x}\leqslant\frac{\mathrm{1}}{\mathrm{4}}\:\wedge{x}\:>\:\mathrm{0}\Rightarrow\mathrm{0}<\:{x}\:\leqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{solution}\:\mathrm{is}\: \\ $$$${x}\in\:\left(\mathrm{0},\:\frac{\mathrm{1}}{\mathrm{4}}\right]\:\cup\:\left[\:\frac{\mathrm{1}}{\mathrm{3}},\infty\right)\:\bigstar \\ $$
