Question Number 96467 by john santu last updated on 01/Jun/20
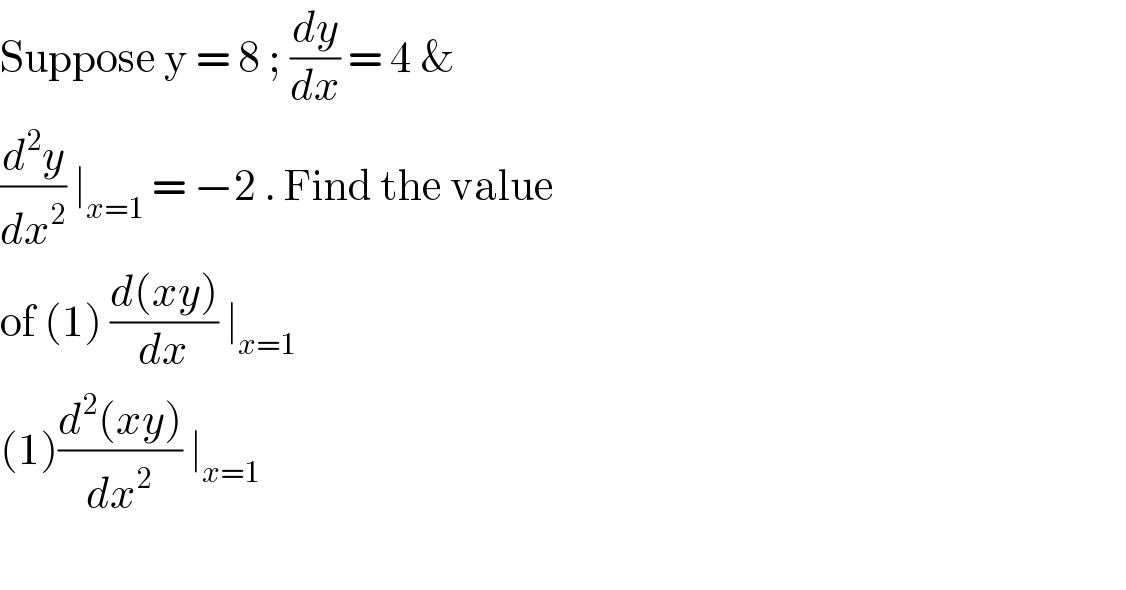
$$\mathrm{Suppose}\:\mathrm{y}\:=\:\mathrm{8}\:;\:\frac{{dy}}{{dx}}\:=\:\mathrm{4}\:\&\: \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:\mid_{{x}=\mathrm{1}} \:=\:−\mathrm{2}\:.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\left(\mathrm{1}\right)\:\frac{{d}\left({xy}\right)}{{dx}}\:\mid_{{x}=\mathrm{1}} \\ $$$$\left(\mathrm{1}\right)\frac{{d}^{\mathrm{2}} \left({xy}\right)}{{dx}^{\mathrm{2}} }\:\mid_{{x}=\mathrm{1}} \: \\ $$$$ \\ $$
Answered by Sourav mridha last updated on 01/Jun/20
![(1)[x(dy/dx)+y]_(x=1) =[4x+8]_(x=1) =12 (2)[x(d^2 y/dx^2 )+2(dy/dx)]_(x=1) =6](https://www.tinkutara.com/question/Q96476.png)
$$\left(\mathrm{1}\right)\left[\boldsymbol{{x}}\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}+\boldsymbol{{y}}\right]_{\boldsymbol{{x}}=\mathrm{1}} =\left[\mathrm{4}\boldsymbol{{x}}+\mathrm{8}\right]_{\boldsymbol{{x}}=\mathrm{1}} =\mathrm{12} \\ $$$$\left(\mathrm{2}\right)\left[\boldsymbol{{x}}\frac{\boldsymbol{{d}}^{\mathrm{2}} \boldsymbol{{y}}}{\boldsymbol{{dx}}^{\mathrm{2}} }+\mathrm{2}\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}\right]_{\boldsymbol{{x}}=\mathrm{1}} =\mathrm{6} \\ $$
